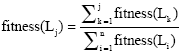Research Article
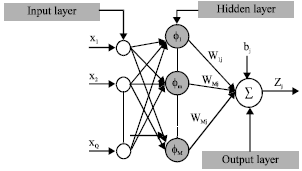
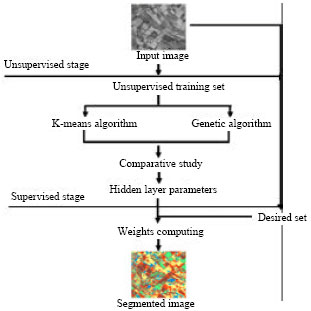
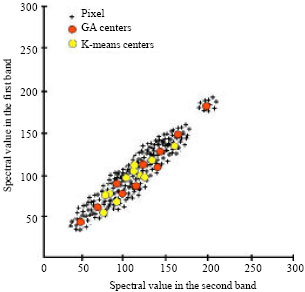
Segmentation of Satellite Imagery using RBF Neural Network and Genetic Algorithm
Centre des Techniques Spatiales, Division Observation de la Terre, 31200, Arzew, Algerie
H.F. Izabatene
Laboratoire Signal Image Parole SIMPA, Department of Computer Science, Faculty of Science, University of Science and Technology of Oran, USTO, Algeria, BP 1505 Oran El M�naouer, Algerie