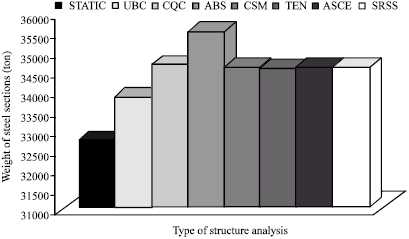
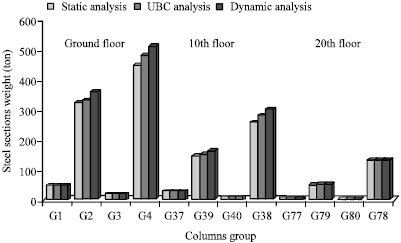
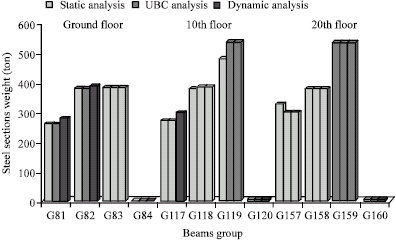
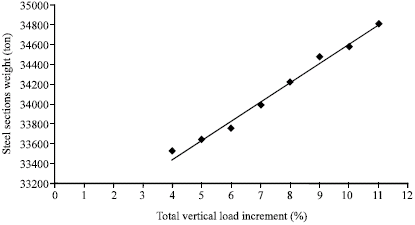
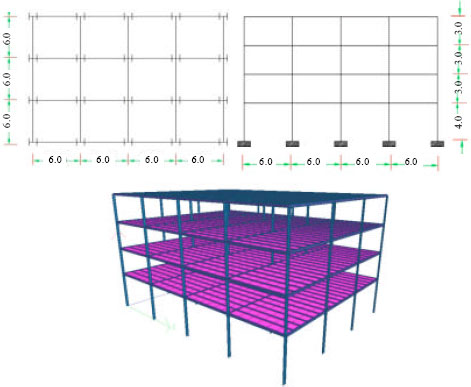
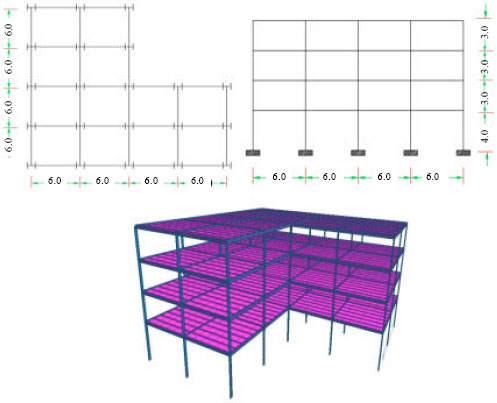
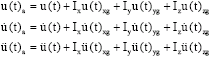Research Article
Effect of Dynamic Analysis and Modal Combinations on Structural Design of Irregular High Rise Steel Buildings
Department of Civil Engineering, College of Engineering, University of Mosul, Iraq
T.E. Saaed
Department of Civil Engineering, College of Engineering, University of Mosul, Iraq