ABSTRACT
Our purpose in this research is to show how much Fermat equation is rich in analytic applications. Effectively, this equation allows to build amazing sequences, series and numbers. The question of the elementary proof of the theorem remains of course, we will see it in this communication. We will make also an allusion tothe very known Fermat numbers
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/aja.2008.15.24
URL: https://scialert.net/abstract/?doi=aja.2008.15.24
INTRODUCTION
We show that Fermat equation allows to build rational sequences and series. After the formulation of those sequences and series, we calculate their limits. We generalize the sequences and series and their limits to Beal equation and to a generalized Diophantine equation. We define also complex sequences. Of course, all the development is available for other Diophantine equations, we show an example, but there are many others, like Pilai, Catalan and Smarandache equations.
THE SEQUENCES
Fermat equation is
Un=Xn+Yn
GCD(X,Y) =1
We will consider in this study two equivalent equations. Effectively, let us pose
x = UnXn
y = UnYn
z= XnYn
After a little calculus
(1) |
And
(2) |
We deduce that if U, X, Y, are integers verifying Fermat equation, then u, x, y, z as defined verify simultaneously the new Fermat Eq. 1 and 2 which follow:
Lemma 1
u=x+y | (3) |
(4) |
Let us build the sequences. If we pose
x1 = xy1 = y
And ![]() integers
integers ![]() verifying
verifying
![]()
And
![]()
Then
![]()
And
![]()
We pose
![]()
Also
![]()
We pose
![]()
And
![]()
Which means that
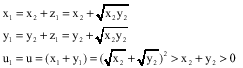
and
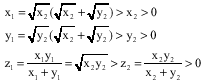
Because ![]() verifying
verifying
![]()
The process is available until infinity. For i
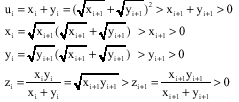
And of course
![]()
We have built the sequences.
Lemma 2
| (H) | |
| (H`) |
Proof of Lemma 2
By traditional induction, for i = 2
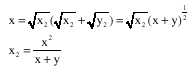
Also
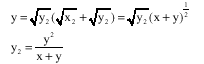
We suppose (H) and (H`) true for i, then
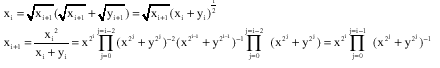
Also
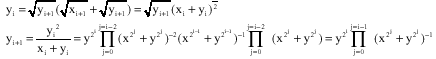
It is proved, but ![]()

Then, for x ≠ y

Lemma 4
Fermat equation has the constant
![]()
As we saw
![]()
It implies the following sum
![]()
then
![]()
And the limits, if x>y
![]()
And
![]()
If x < y
![]()
![]()
Let us study series.
![]()
And if x < y then
![]()
The Applications of the Sequences and the Series
We will consider firstly that x>y
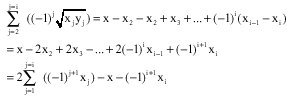
Also

Then
![]()
And
![]()
We will study now the convergence of the series. As ![]() is convergent and
is convergent and ![]() and
and

Is convergent. It implies that ![]() is convergent. Then
is convergent. Then ![]()
It means one thing: ![]() and x-y = 0, then
and x-y = 0, then![]() . It is confirmed by the fact the limit of the general term of the series (here x-y) is equal to zero, because
. It is confirmed by the fact the limit of the general term of the series (here x-y) is equal to zero, because![]() is convergent. And
is convergent. And ![]() and X = Y = 0, because
and X = Y = 0, because
GCD(X,Y)=1 (The reasoning is the same for x < y)
Our question is now: Why are there solutions for n = 2? The answer is in the equations. Effectively, there are trivially an infinity of solutions for n = 1. But the sequences for n = 1 are as it follows;

these are the expressions of the sequences and they do not guarantee the existence of the series for i = 2. So, the case n = 2 is the only exception.
Other Applications of the Sequences and the Series
Let the Beal equation Uc = Xa+Yb; GCD (X,Y) = 1. If we pose
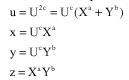
Then
u=x+y | (5) |
And
(6) |
Equation 5 and 6 are the new Fermat equations, they imply after the same reasoning and formulas than for Fermat equation x-y = Uc (Xa-Yb) = 0
Which means
X = Y = 0
Because GCD (X,Y) = 1
Then Beal equation has not solutions, with the same calculus and reasoning than for Fermat equation, for c>2 and a>2 and b>2.
Now, let the general following equation
![]()
GCD(Xk) =1
We pose
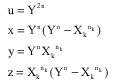
With k = 1,2,…,i
Then
u = x+y | (7) |
| (8) |
Equation 7 and 8 are the new Fermat equation, generalized equation has no solution for n>i (i-1) and nk>i (i-1) other than
![]()
Then
X = Y = 0
Because GCD (Xk) = 1
The new Fermat equations must be used with precaution, for example for the following equation
kUn = Xn+Yn
There are solutions for k = 7 and there are not for k = 2. We must pose judiciously
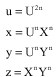
And the new equations are
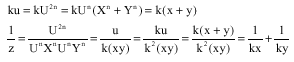
Which are not new Fermat equations and have not the same solutions. It is false to pose

CONCLUSION
The new Fermat equations allow to build sequences and series which allows to test the impossibility of the resolution of an equation. If they are a consequence of some Diophantine equations, they remain an intellectual building. They must be used with precaution, but they are very efficient.
Generalization
Now, we will generalize the results. Let the following equation
| (E) |
We will prove that this equation has not solution for
![]()
When n ≤ i (i−1), nk ≤ i (i−1), there are solutions, for example
i = 2 has 32+42 = 52
i = 3 has 32+42+52 = 63
| 958004+2175194+4145604 = 4224814 |
i = 4 has 275+845+1105+1335 = 1445
It seems to have solutions only for i+1, but we will prove that it is for i (i-1)
We will suppose that Xk are coprime, let
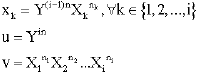
Lemma 5
(9) | |
 | (10) |
We will define the sequences
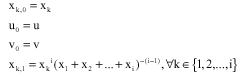
Which implies

The reasoning is available until infinity. Then
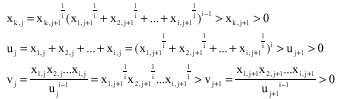
Lemma 6
(P) is the following expression
![]()
Proof of Lemma 6
By traditional induction, it is verified for j=1, we suppose that (P) is true for j, so
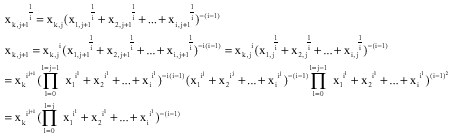
And it is true for j+1.
Lemma 7
The equation (E) conducts to an impossibility, effectively, if we pose
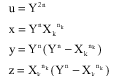
u, x, y and z verify the lemma 1
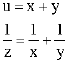
Which conducts, we saw it, to
![]()
Because they are coprime. Now, the question is: why are there solutions for
![]()
Let us pose
![]()
The expression (P) becomes
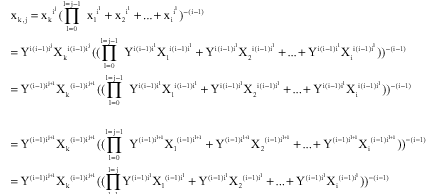
It is the expression for the exponent (i-1). If there are solutions for the exponent (i-1), there will be solutions for the exponent i(i-1). It is not true for i, because of the exponent –(i-1) in the expression (P).
CONCLUSION
The sequences and the series as we defined them have several applications in several diophantine equations, we saw Fermat and Beal, we saw the generalized equation (E), but there are many others like Pilai, Smarandache, Catalan… They are truly very amazing !
THE ALGEBRAIC APPROACH
Now, let Fermat equation
![]()
We pose
![]()
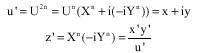 | (11) |
(12) |
We will build sequences
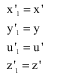
And
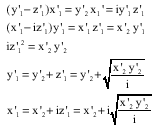
And

And
![]()
The expressions are
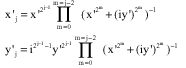
We prove it by induction, as we did for rational sequences
So
![]()
yj is solution of
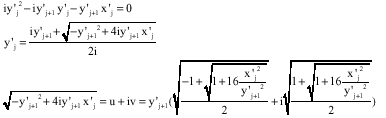
And
![]()
It means that
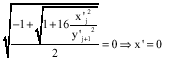
Also for x'j
So the only solution is
x = y = 0
CONCLUSION
It appeared since the beginning, before the change of the data, that the equation contains a symmetry between x and y. Effectively, we found u = x+y. We broke the symmetry by changing the equation in two equations u = x+y and ![]() We have solved the equation and found a method of resolution of Beal equation The conclusion is that Fermat equation (E) conducts always to an impossibility. It is also the case of Beal equation and generalized Fermat equation.
We have solved the equation and found a method of resolution of Beal equation The conclusion is that Fermat equation (E) conducts always to an impossibility. It is also the case of Beal equation and generalized Fermat equation.








