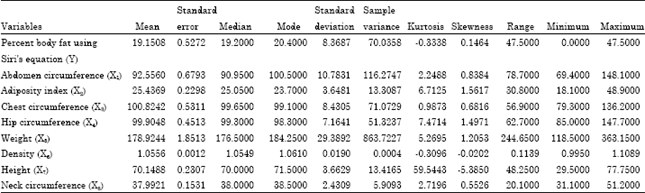
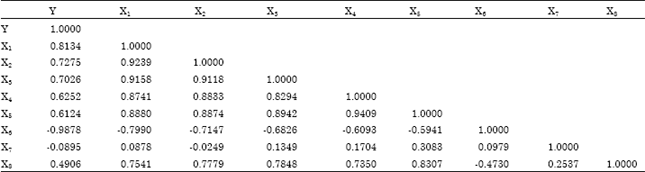
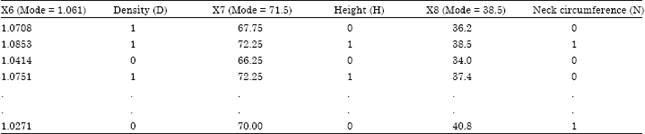
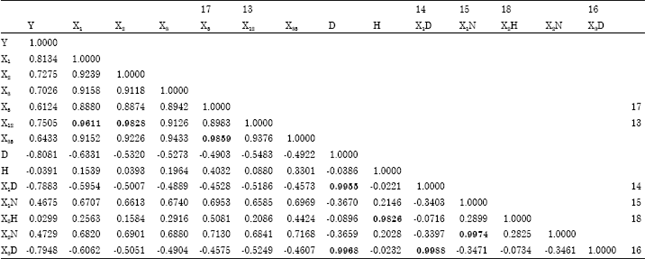
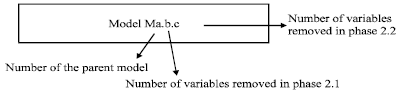
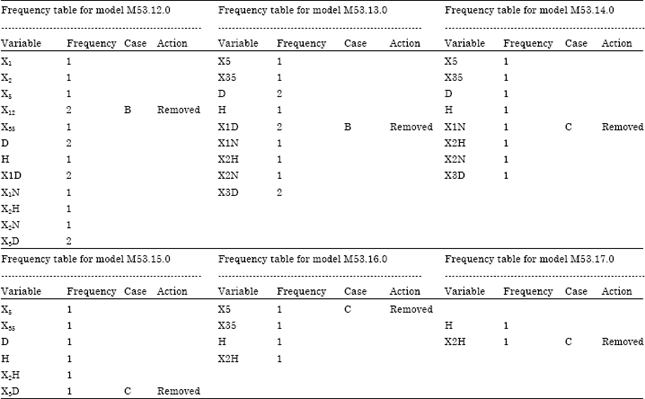
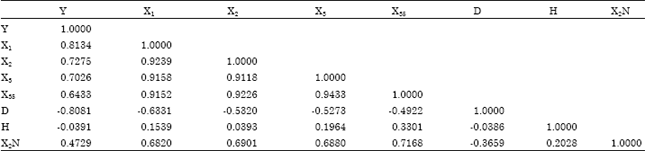
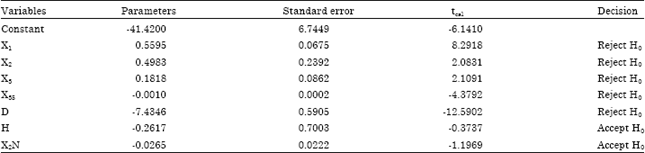
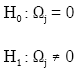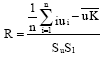Research Article
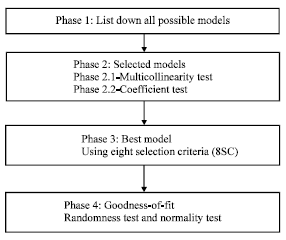
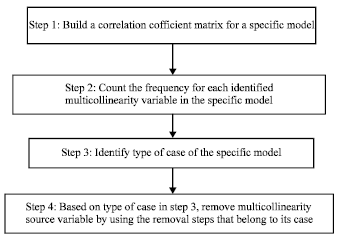
An Alternative Multicollinearity Approach in Solving Multiple Regression Problem
School of Science and Technology, Universiti Malaysia Sabah, 88400 Kota Kinabalu, Sabah, Malaysia
A. Noraini
School of Science and Technology, Universiti Malaysia Sabah, 88400 Kota Kinabalu, Sabah, Malaysia
S.J. Yap
School of Science and Technology, Universiti Malaysia Sabah, 88400 Kota Kinabalu, Sabah, Malaysia