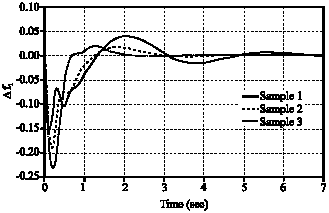
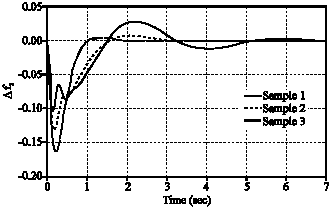
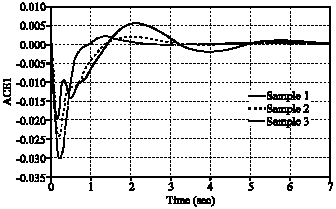
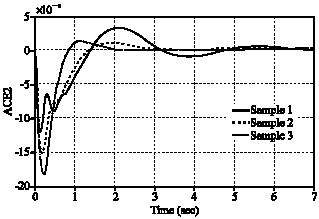
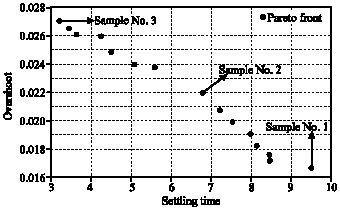
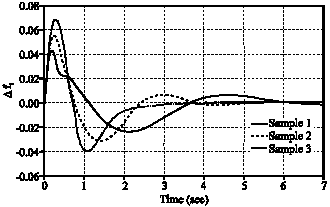
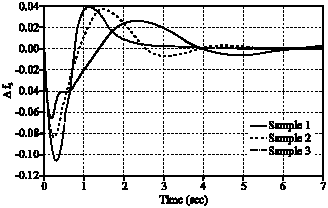
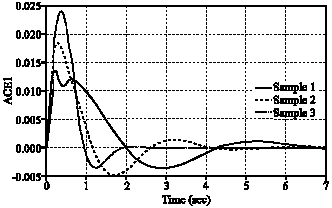
Research Article
Load Frequency Control in Interconnected Power System Using Multi-Objective PID Controller
Young Researcher Club, Islamic Azad University, Ardabil Branch, Danesh Street, Ardabil, Iran
A. Sharifi
Islamic Azad University, Science and Research Branch, Hesarak, Tehran, Iran
M. Aliyari Sh.
K.N. Toosi University, Seyyed Khandan, Shariati Street, Tehran, Iran
M. Teshnehlab
K.N. Toosi University, Seyyed Khandan, Shariati Street, Tehran, Iran
M. Aliasghary
Istanbul Technical University, Istanbul, Turkey