Research Article
Optimum Cost of Prestressed and Reinforced Concrete Beams using Genetic Algorithms
Department of Civil Engineering, The Islamic University of Gaza, Palestine
Mohammed Arafa
Department of Civil Engineering, The Islamic University of Gaza, P.O. Box 108, Palestine
Mohammed Ismail
Department of Civil Engineering, The Islamic University of Gaza, P.O. Box, Gaza, Palestine









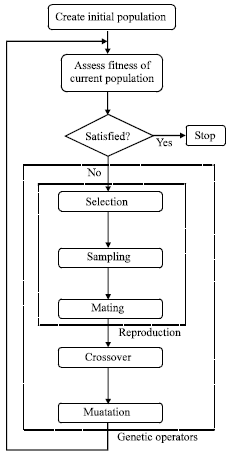
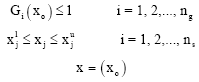
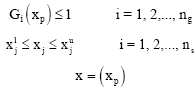
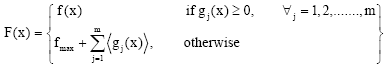








fathi abdelazeem abdelmgeed basioni Reply
it's very wonderful parer and thank you very much
i want another papers about this subject
prakash T Reply
Hi
my self prakash, am doing Ph.D in optimal Design of prestress concrete structures. please help me how to create the objective function and how will you use the mat lab software.