ABSTRACT
The clearances that exist in the mechanism will lead to the motion deviating from ideal movements, meanwhile reducing the kinetic accuracy of mechanical. In order to investigate the output motion error of the offset slider-crank mechanism with clearances, the dynamic equation and virtual prototype model is established based on the impact-pair model and the kinematics characters of the mechanism are analyzed. With the established model, the optimization of the design parameters is proposed to recover the minimum value of the error. The result can predict the dynamic characteristics of mechanism and effective improve the motion precision of the mechanism.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/itj.2013.2390.2397
URL: https://scialert.net/abstract/?doi=itj.2013.2390.2397
INTRODUCTION
The slider-crank mechanism is used to convert rotary motion to linear motion which can transmit motion or force and is widely used in a variety of machinery and equipment, such as vibrating sieve, stamping machinery and internal combustion engines. With the development of modern industry, the operating speed and load capacity of the slider-crank mechanism is been put forward higher requirements. In most cases, the joints of the mechanism exists clearance due to manufacturing errors, material deformation and abrasion. The clearance lead actual movements deviate from ideal movements of the mechanism and cause the impact dynamic load, especially in the high-speed mechanism and this situation leads to decrease in mechanical performance. At present, many designers have focused on investigating the effects of joint clearance on different mechanical systems. Flores et al. (2006) presented a method for the analysis of mechanism with joints clearance and adapted the method to analyze and calculate a slider-crank mechanism with one joint clearance between the piston and connecting rod. Erkaya et al. (2007) considered an especial slider-crank mechanism which add an additional eccentric link between connecting rod and crank and analyzed the dynamic characteristics of the mechanism. Zhang et al. (2008) used the principle of virtual displacement and optimization to discuss the mapping relation between original error and pose error for the output end of planar mechanism and a mathematical model of the pose error for the output end is presented.
In the past, many designers commonly use the continuous contact hypothesis of two components in the research of mechanism with clearances. This study presents a modified contact collision model and coulomb mechanical model which can describe the friction process in the joint clearances to analyze the dynamics characteristic of mechanism. Based on hybrid contact model, this study establishes offset slider-crank mechanism dynamics equations with two joint clearances and adopts ADAMS to simulate the dynamic characteristics of mechanism and the transmission angle of the mechanism has been optimized.
THE MODEL OF JOINT WITH CLEARANCE
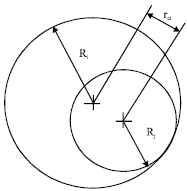
The vector model of joint with clearance: As Fig. 1 show, the gap vector model is established by the introduction of a clearance in the rotation hinge to express the true potential behavior of the joint. In this model, the gap vector represents the precise relative position of the connection point of the two adjacent components which connected by rotating hinge, it can effectively deal with the change in relative position of the clearance joint connection point. The gap vector starts from the rotational center of the bearing and points to the potential contact points when the shaft and the bearing produce a relative movement, the potential contact points constitute the relative collision point of the shaft and the bearing. The size of clearance can reflect whether these two joints are contacted (Guo and Yan, 2007).
 | |
| Fig. 1: | The model of revolute joint with clearance |
The clearance rci is represented by the hole radius Ri and the pin radius Rj, which is expressed as:
| (1) |
The contact collision model of joint with clearance: The contact force model in the process of rotation gap hinged touch collision is an important part of kinetics analysis of the mechanism with clearance. Lankarani-Nikravesh model (Lankarani and Nikravesh, 1990) use a common Hertz contact force expression and take into account the damping effect to describe the energy loss in the collision process. It is shown in Eq. 2:
| (2) |
In Eq. 2, Fn consists of two parts, the first part represents elastic deformation force of the collision process and the second part represents the energy lost in the collision process, while K is equivalent contact stiffness, which is obtained by Goldsmith through the collision experiment of two spherical bodies, which is expressed as:
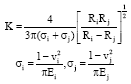 | (3) |
where, v is Poisson ratio, E is Young modulus, Ri and Rj are radius of two spherical bodies.
In Eq. 2, D is damping coefficient and δn is negative element normal deformation. D can be expressed as:
| (4) |
where, ce is coefficient of restitution, δ(¯) is the initial relative velocity of the impact point.
As assumed coefficient of restitution ce≈1 in the derivation of Eq. 4, the expression means that only a large coefficient of restitution, which can not mean that a small coefficient of restitution. The damping coefficient has been improved in the literature (Vogel, 1996), it obtain a corrected Eq. 5 of the relationship between the contact damping and coefficient of restitution:
| (5) |
On the basis of above studies, this article draws on the research ideas of the literature (Calvetti et al., 2004) to create the hybrid model based on Lankarani-Nikravesh model and improved elastic foundation contact model, it is expressed as:
| (6) |
where, Kn is nonlinear stiffness coefficient which can be obtained by solving the slope of the curve between the relationship of the gap hinge load based on the improved elastic foundation contact model and displacement near a transient collision point, it is expressed as:
| (7) |
In the damping force model, by introducing the ratio of the nonlinear stiffness coefficient and Lankarani-Nikravesh stiffness coefficient based on the improved elastic foundation contact model, the damping coefficient Dm is expressed as:
| (8) |
The friction model of joint with clearance: Tangential contact characteristic can be described by the tangential contact force model, in this study, the condition of dry friction is considered rather than lubrication case. The coulomb mechanical model is a currency model to describe the friction action in the case of impact, in order to more accurately represent the dry friction state between the bearing and shaft, this study adopt modified coulomb mechanical model, in which the friction coefficient is a dynamic value rather than a constant and is a function of tangential slip velocity. The tangential contact force Ft is expressed as:
| (9) |
where, vt is the speed tangential component of collision contact point between shaft and hole, μd is dynamic friction coefficient.
THE DYNAMICS MODEL OF SLIDER- CRANK MECHANISM WITH JOINT CLEARANCE
The slider-crank mechanism with joint clearances that mainly composed by crank, connecting rod and slider are shown in Fig. 2. Where, A, B and C are each link point, while link point B and C include clearance. L1 and L2 represent the length of crank and connecting rod. L is the distance of the slider center to the crank rotational center. e is the length of the eccentricity, θ1 and θ2 are the angles between crank and connecting rod and forward x axis. mi and Ji represent each component’s quality and the rotational inertia around the mass center, respectively, G1, G2 and G3 represent mass center position of each component.
Considering the mechanism with joint clearances, the ith joint clearance is expressed use rci, where i = 1, 2, the projection rci,x and rci,y of clearance vector in direction x and y are shown in Eq. 10:
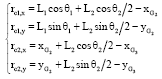 | (10) |
The force components of the pin with clearance to the hole depend on direction x and y can be expressed as Eq. 11:
| (11) |
Azimuth γi can be expressed as:
| (12) |
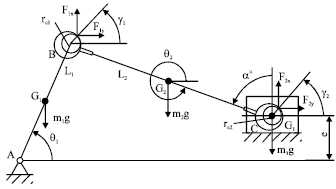 | |
| Fig. 2: | Schematic diagram of offset slider-crank mechanism |
When joints are in collision, the negative elements normal deformation is shown in Eq. 13:
| (13) |
According to Fig. 2, this paper establishes a kinetics equation of slider-crank mechanism with clearance is shown in Eq. 14:
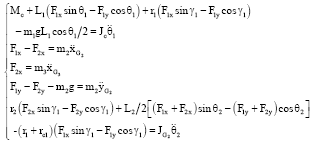 |
where, Mc is the driving moment act on the crack, Jc is the rotational inertia of the crack around rotation center, dynamic differential equations of slider-crank mechanism with clearance can be obtained by all the above equations.
DEVIATION ANALYSIS OF SLIDER -CRANK MECHANISM
Based on joint models and kinetic equation of slider-crank mechanism with clearance established above, the hybrid contact model considering joint clearance was incorporated into the mechanical dynamics analysis software ADAMS to generate the kinetic model (Ge, 2010) of the slider-crank mechanism with clearance, meanwhile, the dynamic characteristics of the mechanism was analyzed (Luo et al., 2010).
According to system model, the software-ADAMS could automatically established Lagrange equation based on the dynamic theory of multi-body system, it can list six Lagrange equation and constraint equation of generalized coordinates with multiplier for each component.
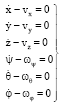 | (14) |
Constraints algebraic equations, external force equation and custom algebraic differential equations are shown in Eq. 15:
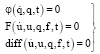 | (15) |
where, q is the generalized coordinate, u is the differential of each generalized coordinates, f is the system external forces and constraints.
Make t = [q, u]T as a state vector, the equations of system can be expressed as:
| (16) |
As shown in Fig. 3, the virtual prototype model of offset slider-crank mechanism is established with ADAMS (Li, 2006) and the physical parameters are shown in Table 1.
The radius of the shaft and the hole of two joint with clearances are 7.5 and 8 mm, respectively. Contact constraint is defined between bearing and shaft in the joint with clearance.
Drive over the slider-crank mechanism, the rotation speed is set to 600 rpm, the dynamic simulation for mechanism with clearance and ideal mechanism without clearance is carried out and the results are shown in Fig. 4 and 5.
The kinematics characteristic curve of the connecting rod and slider are shown in Fig. 4 and 5, in which the upper-left view is the motion curve of ideal mechanism without joint clearance, the upper-right view is the motion curve of mechanism with joint clearance and the underside view is the error curve. In Fig. 4 and 5, P.x is the displacement curve in x direction, V.x is the speed curve in x direction, A.x is the acceleration curve in x direction.
From Fig. 4, under ideal conditions, the displacement, velocity and acceleration curves of the connecting rod centroid in x direction are relatively smooth, however, for the mechanism with clearance, the velocity and acceleration curves are volatile in addition to the displacement curves are essentially coincident. From the deviation curve, the displacement deviation of the connecting rod centroid in x direction is within ±0.5 mm, velocity and acceleration deviation is larger in the beginning stages. From Fig. 5, the displacement deviation of the slider centroid is within ±1.0 mm, it is because that the deviation depends on the clearance vector of two joints. The acceleration of the slider has a larger deviation, these deviations result in a sudden change of direction of the inertial force and will reduce the transmission efficiency of the mechanism.
The acceleration curves of the connecting rod centroid in stable state is shown in Fig. 6, when considering joint clearance, these curves have obvious fluctuation and many peaks, those amplitudes are bigger than that of ideal mechanisms. The analysis shows that due to the existence of clearance between the shaft and sleeve, a gap collision force which is a local effect is generated and each collision time is extremely short, therefore, it has little effect on the displacement, but has obvious influence on the acceleration. The collision force of the clearance joint C are shown in Fig. 7, this is because the existence of clearance which make pulsed contact collision power which reflects the characteristic of high-frequency oscillation in joints.
| Table 1: | Parameters of paver screed |
 | |
 | |
| Fig. 3: | The model of offset slider-crank mechanism with clearances |
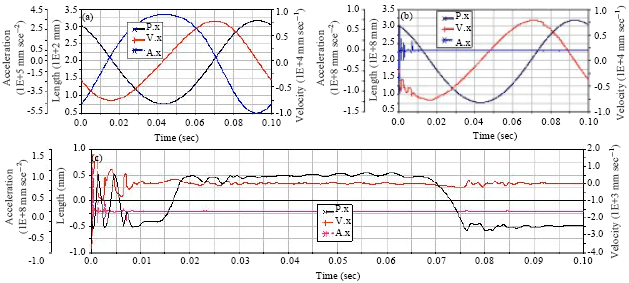 | |
| Fig. 4(a-c): | X-inertia curve and the deviation curve of connecting rod centroid in two conditions (a) With clearance (b) Without clearance and (c) Error |
 | |
| Fig. 5(a-c): | X-inertia curve and the deviation curve of slider centroid in two conditions (a) With clearance (b) Without clearance and (c) Error |
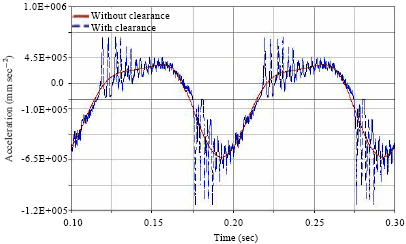 | |
| Fig. 6: | Acceleration of the slider in x direction |
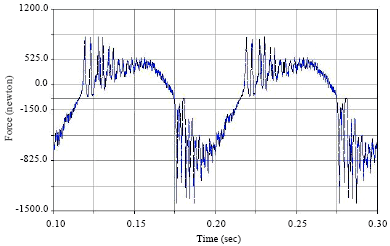 | |
| Fig. 7: | The collision force of the clearance joint C |
 | |
| Fig. 8: | The curve of driving moment applied to the system |
The driving moment curve that is shown in Fig. 8 reflects the same characteristic.
As shown in Fig. 9, the pin centre trajectory relative to the bearing centre at joint C is concerned. In the beginning, the movement of the pin is disordered and has greater impact on the bearing wall and the performance is having a certain penetration depth, when stabilized, the movement of the pin is substantially along the wall surface of the bearing and has a slight fluctuation and the contact force varies along the radial direction.
OPTIMIZATION OF THE TRANSMISSION ANGLE
Transmission angle is an important parameter in the mechanical design and denotes the quality of motion transmission in a mechanism and it is mainly used to obtain the better results for various linkage applications.
 | |
| Fig. 9: | The pin centre trajectory relative to the bearing centre at joint C |
If transmission angle deviation which caused by joint clearance of mechanism is too large, the mechanism will have poor motion characteristics, such as noise and vibrations during high speed operation.
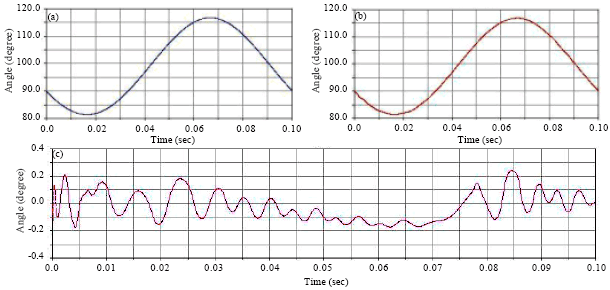 | |
| Fig. 10(a-c): | The transmission angle and deviation curve in two conditions (a) With clearance, (b) Without clearance and (c) Error |
Transmission angle of ideal mechanism a and that of mechanism with joint clearance αu are expressed as:
| (17) |
| (18) |
The transmission angle and deviation curve of the ideal mechanism and mechanism with joint clearance are shown in Fig. 10.
Based on the offset slider-crank mechanism model established in this study, the transmission angle is been optimized. The work scope of the slider-crank mechanism model as shown in Fig. 3 is 110 mm = L1 = 130 and 390 mm = L2 = 410 mm, the eccentricity of the mechanism remains the same. The design variables are x = [L1, L2]T = [x1, x2]T. The aim of this objective function is minimizing the transmission angle error arising from joint clearances in the mechanism. Therefore, the objective function with the principle of a minimum mean square error of the transmission angle is established:
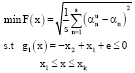 | (19) |
where, αu and α denote the transmission angles of ideal mechanism and actual mechanism with clearance, s is the number of considered points. G1(x) is the linear inequality constraints, x1 and xk are the lower and upper bounds of these variables, respectively.
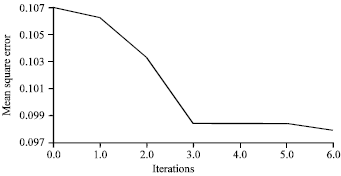 | |
| Fig. 11: | Optimization iteration graph |
Using ADAMS software to optimize the model, step number is 20000. The curve of each iteration value of the objective function is shown in Fig. 11, it can be seen from the figure that after 6 iterations, the optimized values of the mechanism is obtained, the value is 0.097966, which is 8.44% less than the original mechanism.
DISCUSSION
Usually there are joint clearances between the bearing and the shaft of the transmission mechanism, the existence of clearances will reduces the kinematics accuracy of the mechanism and produces vibration and noise. So, it is very necessary to research the effects of joint clearance on mechanical.
The present study are commonly based on the continuous contact hypothesis of two components, while, compared with that, the hybrid contact model is more accurate to simulate the impact and friction between the bearing and the shaft, due to it take into account the physics and geometrical characteristics of internal contact surface of joint. In this study, an improved hybrid model of clearance is embedded into the ADAMS software to analyze the dynamic of the offset slider-crank mechanism. In addition, the design parameters of mechanism have been optimized by using ADAMS software. The result is able to effectively predict movement and improve the transmission performance of the mechanism.
CONCLUSION
In this study, we consider the condition of crank pin and connecting rod center with joints clearance, adopt an improved hybrid model of clearance nonlinear contact force to study how joint clearance affect the dynamic characteristic of offset slider-crank mechanism and analyze the deviation of the mechanism by using ADAMS software. It can be seen clearly from the displacement deviation curve of each member, the kinematic contribution of the previous joint clearance is superposed to the kinematics of the successive joint. In motions initial stage, the movement of the pin is disordered and has greater collision on the bearing wall and the deviation curve of velocity and acceleration have great error, when the mechanism is stable, the movement of the pin is substantially along the wall surface of the bearing and has a slight fluctuation and the slider acceleration curve has obvious fluctuations and a great peak and these effects make the transmission performance degradation. By the optimization of design parameters of mechanism using ADAMS software, the transmission angle error decreases by 8.44%, this result can effectively improve the accuracy of mechanical motion and force transmission efficiency. Considered the joint clearance can more true reflection of the dynamics of the mechanism, and be able to accurately predict the dynamics characteristics of mechanism, it could provide a reference for the research of movement precision and mechanical design for the mechanism.
ACKNOWLEDGMENTS
The research work is supported by A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
REFERENCES
- Calvetti, D., L. Reichel and A. Shuibi, 2004. L-curve and curvature bounds for Tikhonov regularization. Numer. Algorithms, 35: 301-314.
CrossRefDirect Link - Erkaya, S., S. Su and I. Uzmay, 2007. Dynamic analysis of a slider-crank mechanism with eccentric connector and planetary gears. Mech. Mach. Theory, 42: 393-408.
CrossRef - Flores, P., J. Ambrosio, J.C.P. Claro, H.M. Lankarani and C.S. Koshy, 2006. A study on dynamics of mechanical systems including joints with clearance and lubrication. Mech. Mach. Theory, 41: 247-261.
CrossRefDirect Link - Guo, P. and S. Yan, 2007. Monte Carlo simulation of motion errors for four-bar linkages with clearances. J. Tsinghua Univ., 47: 1989-1993.
Direct Link - Lankarani, H.M. and P.E. Nikravesh, 1990. A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des., 112: 369-376.
CrossRef - Luo, T., X. Gan and W. Luo, 2010. Nonlinear dynamics simulation of compacting mechanism with double-eccentric vibrator of asphalt-paver. Proceedings of the International Conference on Intelligent Computation Technology and Automation, Volume 2, May 11-12, 2010, Changsha, pp: 800-803.
CrossRef - Vogel, C.R., 1996. Non-convergence of the L-curve regula rization parameter selection method. Inverse Problems, 12: 535-547.
CrossRefDirect Link








