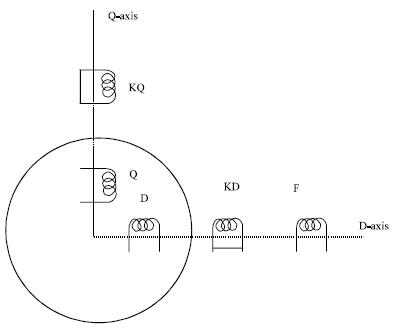
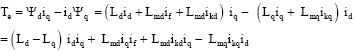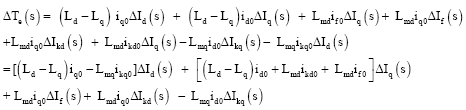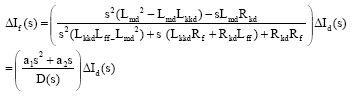Research Article
Analysis of Steady State Stability of a Csi Fed Synchronous Motor Drive System with Damper Windings Included
Department of Electrical and Electronics Engineering, Birla Institute of Technology and Science, Pilani-Dubai, P.O. Box: 345055, Plot No. UG 06, Dubai International Academic City, Dubai, UAE
Sunil Thomas
Department of Electrical and Electronics Engineering, Birla Institute of Technology and Science, Pilani-Dubai, P.O. Box: 345055, Plot No. UG 06, Dubai International Academic City, Dubai, UAE
Ruchira Chatterjee
Department of Electrical and Electronics Engineering, Birla Institute of Technology and Science, Pilani-Dubai, P.O. Box: 345055, Plot No. UG 06, Dubai International Academic City, Dubai, UAE