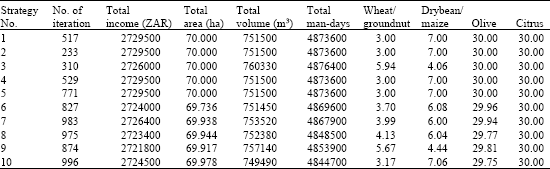
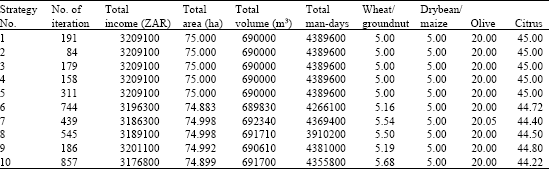
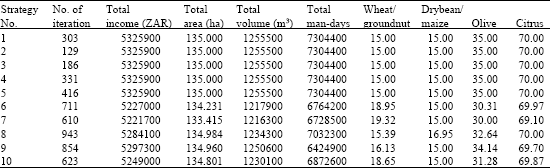
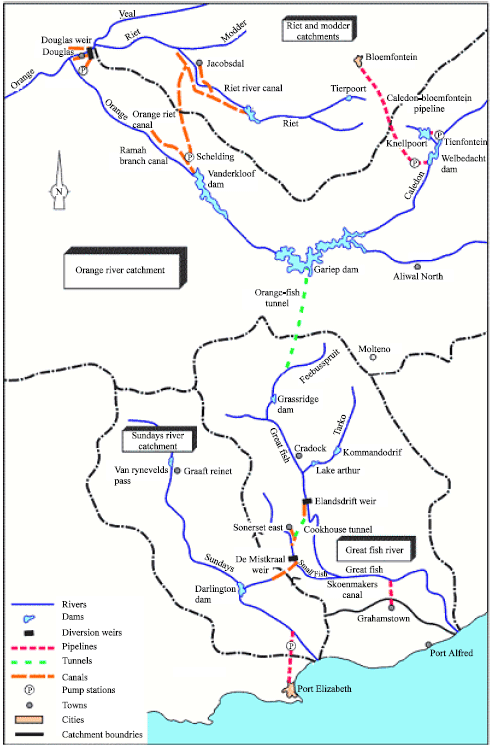
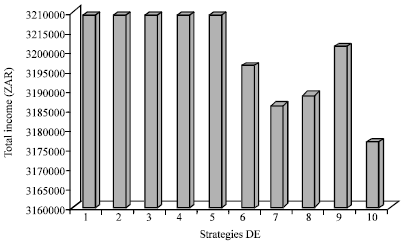
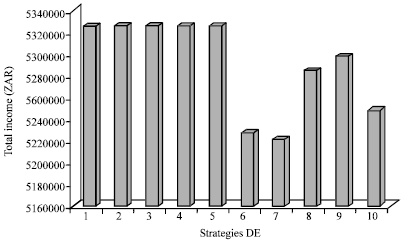
Research Article
Strategies of Differential Evolution for Optimum Cropping Pattern
Department of Civil Engineering, Tshwane University of Technology, Private Bag X680, Pretoria, 0001, South Africa
J.A. Adeyemo
Department of Civil Engineering, Tshwane University of Technology, Private Bag X680, Pretoria, 0001, South Africa