Research Article
Geologically-Constrained Fuzzy Mapping of Porphyry Copper Mineralization Potential, Meiduk District, Iran
Department of Geology, Shahid Bahonar University, Kerman, Iran
A. Mehrabi
Geological Survey of Iran, Kerman, Iran
Using binary predictor patterns for mapping mineral potential assumes a crisp boundary between favorable and unfavorable ground (Carter, 1989, 1994; Carranza and Hale, 2000). In most real cases, however, the boundary between grounds that are favorable and unfavorable for the occurrence of mineralization is imprecise (Carranza and Hale, 2003). Classifying mineral potential, therefore, requires a method capable of using imprecise concepts where a precise boundary membership or non-membership in a class of spatial evidence of mineral potential may be impossible or impractical. One such method is the application of the Dempster-Shafer evidential belief theory (Moon, 1990; An et al., 1992). Carter and Cheng (2008) and An et al. (1994) showed that representation of multi-class sets of spatial evidences of mineral potential using evidential belief functions can only be either data-driven or knowledge-driven (although an approach involving incorporation of knowledge to assign weights to multi-class spatial evidences derived through data-driven quantification of spatial associations between mineral deposits and geological features is demonstrated for mapping mineral potential). A partly knowledge-driven and partly data-driven approach to map mineral potential based on multi-class spatial evidences is feasible by the application of the theory of fuzzy sets (Zadeh, 1965).
The method used in this study is based on a fuzzy logic model, which is a partly knowledge-driven and partly data-driven approach. Fuzzy logic can be used with data from any measurement scale and the weighting of evidence is controlled entirely by the expert. This method allows for more flexible combinations of weighted maps and can be readily implemented with GIS modeling language. This is different from data-driven approaches (Carranza et al., 1999; Debba et al., 2009), such as weights of evidence or logistic regression, which use the locations of known deposits to estimate weights or coefficients.
This study which is conducted from Sept. 2008 to Apr. 2009, is concentrated on geologically constrained fuzzy mapping of porphyry copper mineralization potential, in Meiduk District, which is located in is located in the Southern part of Central Iranian Volcanic Belt. There are a few of examples of partly knowledge-driven and partly data-driven applications of the theory of fuzzy sets to mineral potential mapping. Gettings and Bultman (1993) applied the possibility theory from fuzzy logic to the quantification of favourableness of quartz-carbonate vein deposits in Southeast Arizona. They defined conditions necessary for the formation of the deposits and represented each condition as a fuzzy set enumerated in a grid over the area. The intersection of the fuzzy sets measures the degree of simultaneous occurrence of the necessary conditions and provides a measure of the possibility of deposit occurrence. The example of Gettings and Bultman (1993) is based mainly on rock units and their genetic rather than spatial relationships to the known Ag-Pb vein-type deposits; the fuzzy membership functions of the different rock units were subjectively assigned. Cheng and Agterberg (1999) developed a weight of evidence approach based on fuzzy sets and fuzzy probabilities for mineral potential mapping. Instead of separating spatial evidences of mineralization into binary or ternary form, they created fuzzy sets that contain genetic elements. They then defined fuzzy probabilities to construct a model for calculating the posterior probability of a unit area containing mineralization based on the fuzzy evidence for a unit area. Since, in weights of evidence modeling the requirement of conditional independence among the spatial evidences is not always satisfied, Robinson (2000) developed a new technique called vectorial fuzzy logic, based on fuzzy logic principles, for the integration of spatial data for enhanced mineral prospectivity mapping in the Kalgoorlie Terrane, Western Australia. The technique, based on vector mathematics, differs from existing methods of spatial data integration (e.g., Boolean logic, index-overlay, weights of evidence) in that it displays prospectivity as a continuous surface and allows a measure of confidence to be incorporated. The vectorial fuzzy logic technique of Robinson (2000) involves the subjective assignment of fuzzy prospectivity weights and fuzzy measures of confidence weights based on 80 deposits with known production of >500 kg gold. The method of Robinson (2000) is thus applicable to areas with well-known deposits (i.e., with production data) but is not readily applicable to the study areas in this work. This study presented is partly similar to the study of Carranza (2002) and Carranza and Hale (2002) although here the subjective assignment of fuzzy membership values is based on quantified spatial associations between mineral deposits and geological variables as Carranza (2009) has done.
The appropriate geoexploration-datasets (i.e., lithologic units, hydrothermal alteration units, faults/fractures, porphyry pluton contacts/centroids, batholithic pluton margins, locations of mineral deposits, topographic geoinformation) in the study areas were used in mapping mineral potential in the study area through the application of the theory of fuzzy sets. A pixel size of 100x100 m was used in the GIS-based raster analysis.
Fuzzy sets of evidences of porphyry copper potential were created by using weights of evidence method. Then fuzzy membership values for the different sets of spatial evidences were provided. Finally maps of fuzzy membership values were combined for preparing fuzzy predictive mapping of porphyry copper potential. Most of the procedures were carried out using Spatial Data Modeler Extension and GIS software.
Geology of the Area
The study area is located in the Southern part of Central Iranian Volcanic Belt, between 30° 7.5´-30° 30´N latitudes and 55°-55° 30´E longitudes. Meiduk mine is an active porphyry cupper mine there with a 1997.91 km2 area. Figure 1 shows the location of the study area.
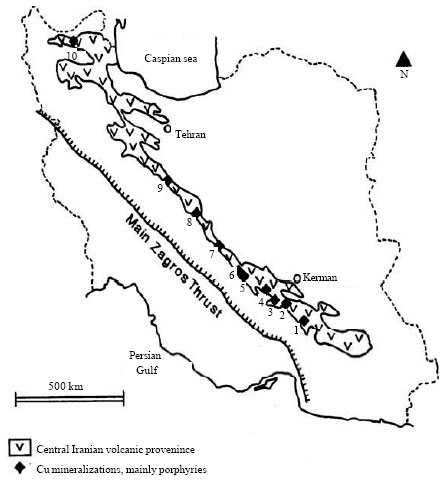 | |
| Fig. 1: | Sketch map showing the position of the Central Iranian volcanic belt and some porphyry-type copper mineralizations of Kerman and Yazd region relative to the main Zagros thrust. 1: Bahraseman, 2: Takht, 3: Kuh Panj, 4: Sar Cheshmeh, 5: Meiduk, 6: Gowde Kolvary, 7: Darrehzereshg, 8 :South of Ardestan, 9: Sharifabad, 10: Sungun (after Shahabpour and Doorandish, 2008) |
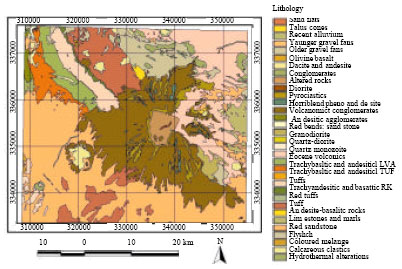 | |
| Fig. 2: | Geological map of Meiduk |
Geological data inputs to the GIS are derived and compiled from geologic maps of various scales. The contacts of mapped lithologic units were hand-digitized into vector format (Fig. 2).
The Central Iranian volcano-sedimentary complex, with Northwest-Southeast direction has 2000 km length and 150 km width extends as the same direction as Zagros (Berberian, 1995; Derakhshani and Farhoudi, 2005; Shahabpour and Doorandish, 2008). The eruption of this belt started in the Cretaceous and in the Eocene it got to its highest activity.
Most of the area we are studying is consisted of volcanic-alluvial parts of Eocene period. One of the dominant features of this area is the great amount of volcanic Eocene rocks that have been under consideration as the main ore creating part (Derakhshani and Abdolzadeh, 2009a). From the middle Oligocene to Miocene, the injection of diorite to granodiorite bodies creates the porphyry copper of the zone and most of related occurrences. Also, in many areas extensive layers have covered these intrusive bodies in guise of little diorites and stock. After that dykes and stocks of diorite-quartz diorite in upper Miocene had been implementing to plutonium cycle in the area (Derakhshani and Abdolzadeh, 2009b).
The study area has three important mines of porphyry copper named as Meiduk, lachah and Chah-Mesi and 81 copper indexes is known in this area (Table 1).
Summarized in Table 2 are the quantified spatial associations between the known porphyry copper deposits and the structural features in the province, using weights of evidence method (Derakhshani and Mehrabi, 2009). The fuzzy membership values for the different sets of spatial evidences of porphyry copper potential are given in Table 3. Therefore, based on this table the maps of fuzzy membership values for the different sets of spatial evidences are prepared. Figure 3 shows the map of fuzzy membership value of pluton centroids. The spatial association between porphyry copper deposits and faults is due to the role of the latter in localizing mineralization. Faults and fractures could provide channel ways for mineralizing fluids whilst igneous intrusions provide heat sources and cause chemical reactions with the intruded rocks that may bring about mineral deposition at or near the intrusive margins/contacts. So map of fuzzy membership value of strike-slip fault fractures of the study are is prepared and shown in Fig. 4.
| Table 1: | Porphyry copper mines, explored deposits and prospects |
 | |
| Table 2: | Optimal spatial associations between porphyry copper deposits and structural features, Meiduk Province |
 | |
| Table 3: | Distance and unit classes and fuzzy membership scores for the different curvilinear or point geological features, lithologic formations and hydrothermal alteration units, study area |
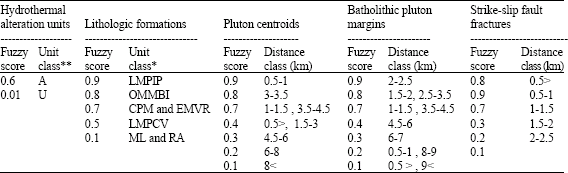 | |
| *LMPIP: L. Miocene-pleistocene intrusive porphyries, LMPCV: L. Miocene-pliocene clastics/volcanics, ML: Miocene limestones; OMMBI: Oligocene-M. Miocene batholithic intrusives, EMVR: Eocene-miocene volcaniclastic rocks, CPM: Cretaceous-paleogene metavolcanics, RA: Recent alluvium. **A: Hydrothermal alteration, U: Unaltered | |
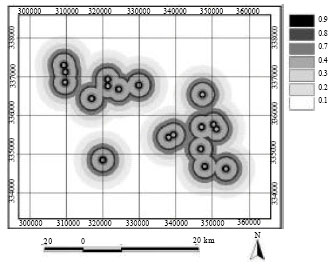 | |
| Fig. 3: | Map of fuzzy membership value of pluton centroids |
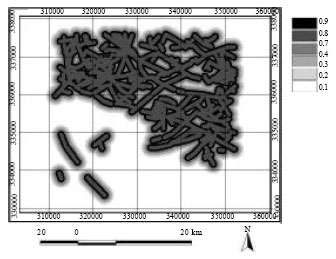 | |
| Fig. 4: | Map of fuzzy membership value of strike-slip fault fractures |
Also, map of fuzzy membership value of batholithic pluton margins of the study area is prepared and shown in Fig. 5. Since, the lithologic formations of the Central Iranian volcanic belt could play essential role in this regard, so the map of fuzzy membership value of lithologic formations of the area is prepared too (Fig. 6). Hydrothermally-altered rocks are a lithologic anomaly, which result from the chemical attack of pre-existing rocks by hydrothermal fluids. The spatial distribution of hydrothermally altered rocks is a key to locating the main outflow zones of hydrothermal systems, which may lead to the recognition of mineral deposits. The mineral images, a digital elevation model image and training pixels of the known hydrothermal alteration units were used in a supervised classification to map fuzzy membership value of hydrothermal alteration units (Fig. 7).
The fuzzy sets are combined in a number of steps to represent intermediate hypotheses regarding the geological significance of the spatial evidences of porphyry copper potential (Fig. 8).
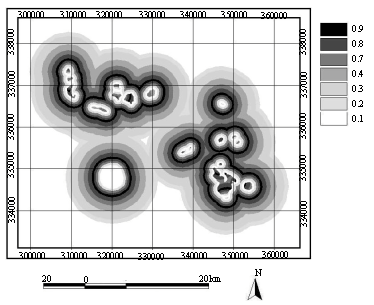 | |
| Fig. 5: | Map of fuzzy membership value of batholithic pluton margins |
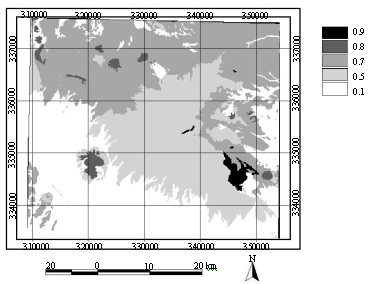 | |
| Fig. 6: | Map of fuzzy membership value of lithologic formations |
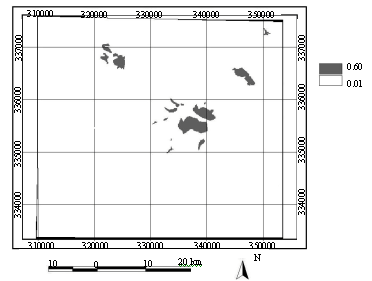 | |
| Fig.7: | Map of fuzzy membership value of hydrothermal alteration units |
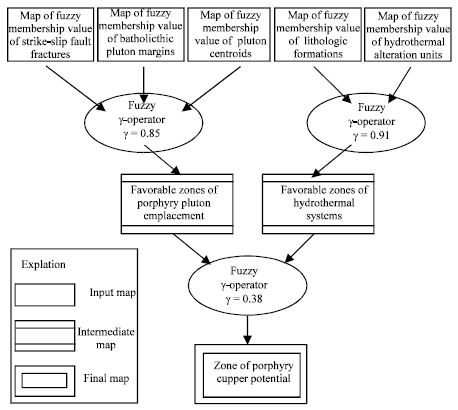 | |
| Fig. 8: | Inference network for producing predictive map of porphyry copper potential |
In classical set theory, the membership of an object in a set of objects is defined as complete (= 1) or non-complete (= 0). In fuzzy set theory, a fuzzy set is defined as a subset of objects whose membership in a set of objects is intermediate between complete membership and non-complete membership. Fuzzy sets are represented by means of membership functions. A membership function, mA(x), is a mapping of the fuzzy membership of x from the universe of discourse X into the unit interval [0,1], thus:
μA (x) : X→ [0,1]
The grade of membership is large (classically equal to 1) for objects that completely belong to the fuzzy set; it is small (classically equal to 0) for objects that do not completely belong to the fuzzy set. For a particular object or class of objects, the more completely it belongs to the fuzzy set, the closer its membership grade is to 1. Thus, individual objects or classes of objects represented in maps can be evaluated regarding their membership in a fuzzy set of geological objects, based on a subjective judgment. Grade of membership is usually represented by a membership function that need not be linear or even continuous; indeed, many fuzzy sets have extremely nonlinear membership functions. The membership always relates to a certain proposition. In mineral exploration, the proposition is favorable location for mineral deposit. In addition, the various fuzzy operators those are useful for combining mineral exploration datasets, namely the fuzzy AND, fuzzy OR, fuzzy algebraic product, fuzzy algebraic sum and fuzzy g-operator.
Generation of Fuzzy Sets
To generate the fuzzy sets of favorable distances to curvi-linear or point geological features, the results of the spatial association analyses were used. Based on the quantified spatial associations between the mineral deposits and the curvi-linear or point geological features, multiple distance classes were defined and fuzzy membership values were assigned to these classes based on subjective judgment.
It is evident from Fig. 8 that there are several possible combinations of fuzzy operations to integrate the fuzzy input maps in order to derive a final fuzzy membership map of favorable zones of porphyry copper potential. We used fuzzy γ-operator to produce a final fuzzy membership map. Figure 8 shows the inference network based on the three hypotheses to predict porphyry copper potential using fuzzy logic as the inference engine. For the first hypothesis, the input maps of fuzzy scores for proximity to strike-slip fault discontinuities, batholithic pluton margins and porphyry pluton centroids were combined to derive an output map of evidence for favorable zones of porphyry pluton emplacement. For the second hypothesis, the input maps of fuzzy scores for favorable host rocks and hydrothermal alteration were combined to derive an output map of evidence of hydrothermal systems. For the third hypothesis, the intermediate output maps of favorable zones of porphyry pluton emplacement and of hydrothermal systems were combined to derive a map of zones of porphyry copper potential. Figure 9 shows the flowchart of procedure Inference network on the input maps.
Therefore, we produce predictive map of porphyry copper potential (Fig. 10). The study area divides to ten classes. The grade of membership is large (classically equal to 1) for objects that completely favorable to porphyry copper potential; the areas that assigned a fuzzy membership values of 0.4 to 0.1 was not favorable to copper potential. So findings of this research correlate with the aim of the project.
However, in the next pace in order to shorten the final potential map andunderstanding which part must be discovered first, from 0 to 0.4 degrees is called without potential area, from 0.4 to 0.7 is called weak, from 0.7 to 0.8 is called average area and from 0.8 to 0.9 is considered on appropriate area of porphyry copper potential.
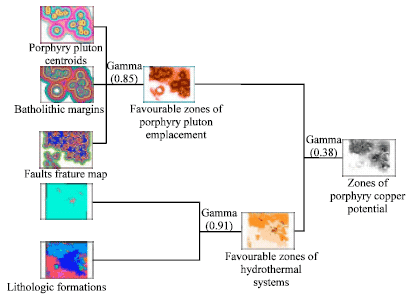 | |
| Fig. 9: | Flowchart of procedure Inference network on the input maps |
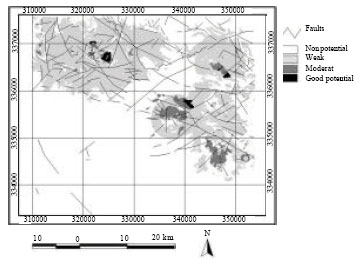 | |
| Fig. 10: | Relation between porphyry copper potential with faults and fractures |
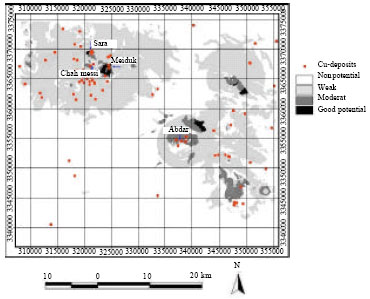 | |
| Fig. 11: | Location of four deposits in relation with cupper potential areas |
According to this ranking, just 7.1 km2 that is 0.35%of the whole area is appropriate, 15.1 km2 that is 0.87% of whole area has average copper potential and 639.1 km2 that is 31.9% of the studied area is in the next rank and 66.88% of the area is without potential. Location of four known deposits is shown in Fig. 11 in relation with cupper potential areas.
There are very little published works on the geologically constrained fuzzy mapping of porphyry copper mineralization potential, in southern part of central Iranian volcanic belt and to the best of our knowledge this is the first study of its kind that concentrates on the quantitative interpretation of this spatial association in the study area by taking advantages of fuzzy mapping and GIS technology. The results of this study strongly agree with the findings of Carranza (2002) in Philippines and Carranza and Hale (2002). Although, here the subjective assignment of fuzzy membership values is based on quantified spatial associations between mineral deposits and geological variables as Carranza (2009) has done. But this is different from data-driven approaches (Carranza et al., 1999; Debba et al., 2009), such as weights of evidence or logistic regression, which use the locations of known deposits to estimate coefficients or weights.
The studied area could be divided into 4 areas: the area with favorable potential (0.35%), the area with average potential (0.87%), the area with weak potential (31.9%) andarea with unfavorable potential of porphyry copper (66.88%). If we overlay the map of porphyry copper potential with the map of faults and fractures, we will find that areas with favorable potential are located in areas of high fractures compression, therefore the effect of fractures in creating porphyry copper is understood. The integrity of the specified areas is confirmed by locating some big porphyry copper deposits like Meiduk, Sara and Chah-Mesi in the favorable zone.
The authors greatly appreciate the scientific comments of Dr. Zarasvandi. Also the authors would like to express their gratitude to Dr. Rangzan for his useful suggestions. We appreciate the critical reading by the arbitration committee and we welcome any enlightening suggestions and insightful comments.