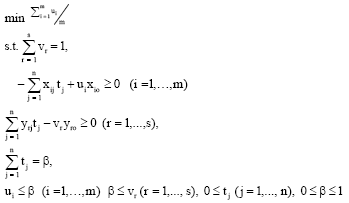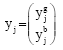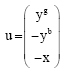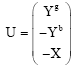Research Article
Supplier Selection using a New Russell Model in the Presence of Undesirable Outputs and Stochastic Data
Department of Industrial Management, Faculty of Management and Accounting, Islamic Azad University, Karaj Branch, P.O. Box 31485-313, Karaj, Iran
Reza Farzipoor Saen
Department of Industrial Management, Faculty of Management and Accounting, Islamic Azad University, Karaj Branch, P.O. Box 31485-313, Karaj, Iran