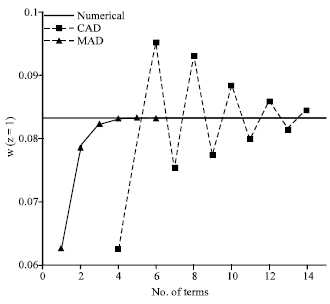
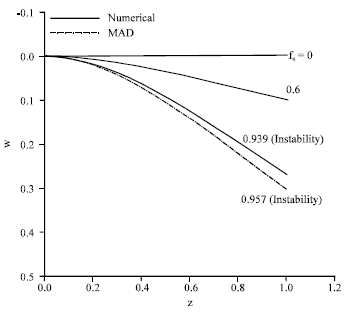
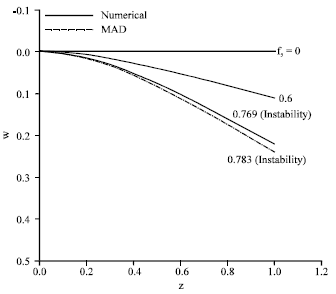
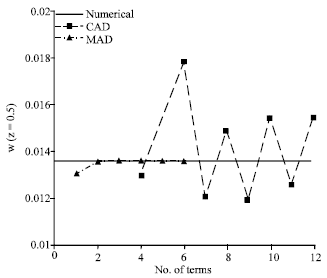
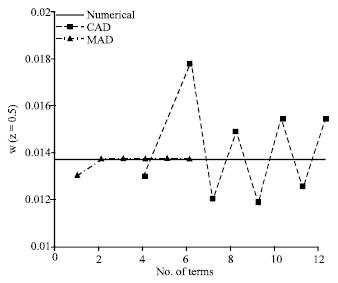
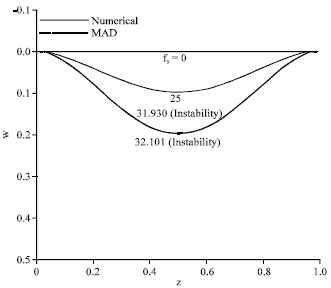
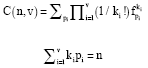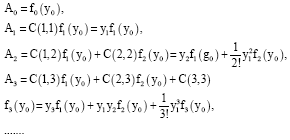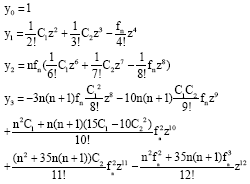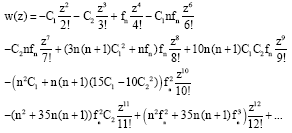Research Article
Evaluating the Ability of Modified Adomian Decomposition Method to Simulate the Instability of Freestanding Carbon Nanotube: Comparison with Conventional Decomposition Method
Mechanical Engineering Group, Naein Branch, Islamic Azad University, Naein, Iran
Mohamadreza Abadyan
Mechanical Engineering Group, Shahrekord Branch, Islamic Azad University, Shahrekord, Iran