ABSTRACT
The RSA algorithm has some important parameters affecting its level of security. It is shown here that increasing the modules length plays an important role in increasing the complexity of decomposing it into its factors. This will increase the length of the public key and the length of the encrypted message making it more difficult to be decrypted without knowing the decryption key. However, the public key length has no major affect on the private key length. When the length of the message is changed then the length of the encrypted message will proportionally change, hence larger chunks are selected to obtain larger encrypted message to increase the security of the data in use.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.60.63
URL: https://scialert.net/abstract/?doi=jas.2005.60.63
INTRODUCTION
When data is transmitted over a certain channel, it is possible that someone else can receive and listen to it. This may include some confidential data like password or so. In wireless communications, this interference is more probable than it is in wired communications, especially if the third party is within the range of transmission.
Encrypting data is mainly used to ensure privacy, such that even if a third party receives the data; he can not listen to it without decryption, the process that requires the knowledge of the encryption keys, which are not available for him. In simple terms, encryption is the process by which information in one form is transformed into another one by use of a certain encryption algorithm. The original information is usually referred to as “plaintext” and the encrypted version is referred to as “ciphertext”. Encryption increases integrity, confidentiality, non repudiation and authentication, which helps in confirming complexity and security as used in satellite communications, banking, network communications, multimedia and cellular communications[1].
Authentication improves the security of the data transfer, since only after a successful authentication, on both sides, the receiver is allowed to see the data.
Basically there are two types of data encryption, block cipher, where data is encrypted in chunks of a specific size, and the stream cipher where each bit of data is sequentially encrypted using one bit of the encryption key[2,3]. This encryption key can be one of two categories, the symmetric encryption where the same key is used for both encryption and decryption, or asymmetric encryption where one key is used for encryption and another one is used for decryption.
Several encryption techniques were presented to secure data transmission[2]. Thus, Cryptanalysis has also been presented, that is the art of deciphering encrypted communications without knowing the proper keys, and this attack function may detect the original message from its encrypted one or from a weak part found in encryption process or even by trail and error.
Hash number is used to improve the security of an encrypted message. The hash value is computed from a base input number using a certain hashing algorithm as illustrated in example 1[4].
Example 1: Let the input number be 10667 and the Hashing algorithm is H= input number * 143 then the Hash value is 1525381.
It is almost impossible to determine that the hash value (1525381) came from a multiplication process of the input number (10667) by 143.
Public keys usually use complex algorithms and very large hash values for encryption, including 40 to 128 bit numbers. A 128-bit number has a possible of 2128 different combinations. This shows how hard it is to detect the key. A basic encryption process is illustrated in Fig. 1.
RSA algorithm and key generation: The security of RSA algorithm is based on the difficulty of factoring large numbers, which is almost impossible for 1024 bit numbers. RSA is a public key cryptosystem for encryption and decryption as well as authentication[5].
 | |
| Fig. 1: | Basic encryption process |
The main functions of an RSA algorithm work as follows:
Step 1: Find two large prime random numbers (p and q) then find their product (n= p q), n is called the modules.
Step 2: Find the encryption key, e, and the decryption key, d, such that they are relative prime to (p-1)(q-1). Hence they must satisfy;
| (1) |
If two numbers are relative prime then their prime factorization do not share. (I. e, 9 and 40 are relative primes because they have no common factors). The values of e and d are called the public and private exponent, respectively. The public key is the pair (n, e); the private key is the pair (n, d). The factors p and q may be destroyed or kept with the private key[6]
Step 3: Encrypt the message number (text or image) using;
| (2) |
Where, m is the message to be encrypted, e is the public key, n is the modules number and c is the resulting ciphertext number.
Step 4: The original message can be retrieved from the encrypted one using;
| (3) |
Where, d is the decryption (secrete) key.
It is conjectured that if n is generated by picking at random two big primes and multiplying them, then factoring n is an intractable problem. Also computing d given e and n is as hard as factoring n. This is the assumption of the RAS; clearly if factoring is easy then RSA assumption fails[7]. The RSA algorithm provides excellent protection of voice and data.
To be able to generate the RSA parameters, one has to decide on the maximum allowed length of each of these parameters. This will be reflected on the security of the system. Initially the prime factors p and q number should be chosen to generate the modules number n. This n should be of a certain length, which is controlled by the generating number (n-bit). Varying this length will successively change the length of both p and q since they are the factors of n.
Another important limit is the maximum allowed length (e-bit) that can be used to generate the public key. Moreover, it is obvious that as the chunk of message m increases then the encrypted message c will also increase[2], hence chose an appropriate value for the length of the block message (cut-length) to be processed at a time. This length will play an important role in increasing the complexity of factoring the encrypted message c to obtain the original message m.
Simulation results: The RSA algorithm is to be analyzed by changing one parameter at a certain time while keeping all other parameters unchanged. The sequential RSA procedure is as follows:
| 1. | Initialization |
| 2. | Dividing the message into blocks of a certain length (cut length) |
| 3. | Encrypting, sequentially, each block of the message |
The initialization process requires some initial information like the total data size and the maximum allowed length of RSA modules n. Then it produces the prime numbers p and q, the modules n and the public and private keys e and d. Once the keys are initialized, the message can be divided into sub blocks each of a certain length such that each of these blocks is treated by itself as shown by Williams[2]. The decryption process takes a reverse order to recover the original message using the encrypted message and the secrete key d as given by Joset et al.[3].
The importance and effect of changing the RSA parameters are analyzed such that one parameter is changed at a certain time and the others are kept fixed. Initially the message is set to “how are you”, the number of e-bit is chosen to be 64 and the cut length is taken to be equal to the whole message length.
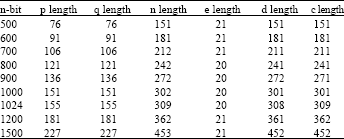
Changing the modules length: Changing the maximum length of the generating number n-bit to generate the modules n will affect the other parameters as shown in Table 1.
It is clearly seen here that increasing the maximum limit on the length of the modules number will increase the length of both p and q factors. Moreover, the length of the secrete key d and the length of the encrypted message c are also increased at the same rate as illustrated in Fig. 2.
| Table 1: | The effect of changing the modules number |
 | |
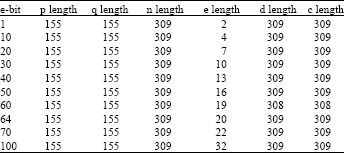
| Table 2: | The effect of changing the limit on the length of the public key |
 | |
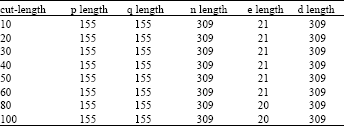
| Table 3: | The effect of changing the cut length |
 | |
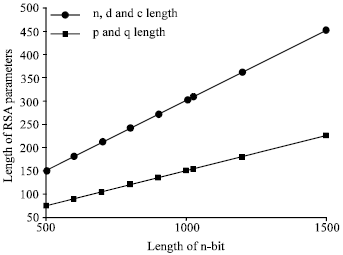 | |
| Fig. 2: | Modules length vs. RSA parameters length |
However, the length of the public key e has remained almost constant since it is controlled by the e-bit length but not by the n-bit length.
As a result, increasing the n-bit length will provide a more secure value for the private key d, since larger d means more security where as the public key e does not have that importance here.
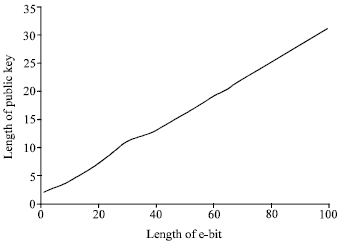 | |
| Fig. 3: | Length of the e-bit vs. Public key length |
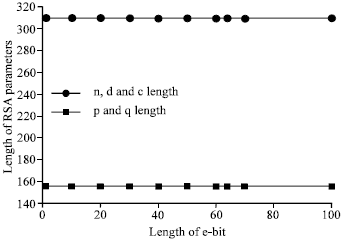 | |
| Fig. 4: | (e-bit) length vs. RSA parameters |
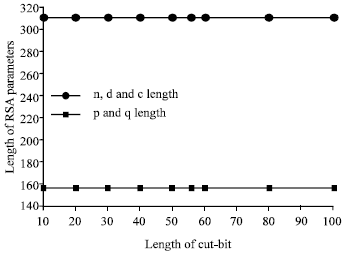 | |
| Fig. 5: | Cut-length vs. RSA parameters |
Changing the public key length: The previous parameters of the algorithm are kept as they are with the module number set to 1024. Changing the maximum limit of the length of the public key (e-bit) affects, mainly, the length of the public key e as illustrated in Table 2.
Thus, Table 2 shows that changing the limit of the public key generation (e-bit) has a direct affect on the public key length but has no major affect on the other parameters as shown in Fig. 3 and 4, respectively. The length of this public key e is proportionally increasing as e-bit increases.
Changing the length of the message to be processed (cut-length): The cut length is the number of characters to be processed at a time, either in encryption or decryption. Here the message is divided into sub blocks each of length equal to cut length. To illustrate the importance of this parameter, the message is taken long enough and the cut length is allowed to vary in both the encryption/decryption process.
Keeping the input data as discussed before where n is set to 1024, e-bit is 64 and choosing a long message like “how are you today? the weather is nice it is suitable for a trip”. Here the total message length is 66. The effect of changing the cut length gives the results as shown in Table 3. Obviously, the values of p, q, n, e and d are independent of the cut-length as illustrated in Fig. 5.
CONCLUSION
The RSA algorithm consists of some high order mathematical operations performed on some parameters in a certain order. These parameters control the level of security of the encrypted data. It was shown here that complexity of decomposing the modules into its factors is a function of the modules length itself. The importance of this length is also reflected on the security of the public key making it more difficult to be detected.








