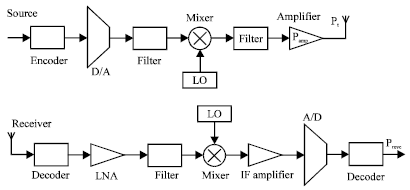
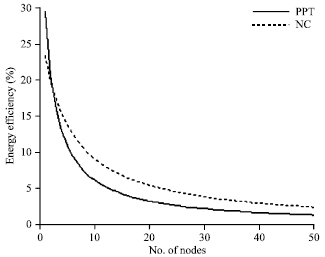
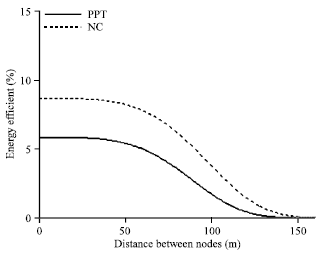
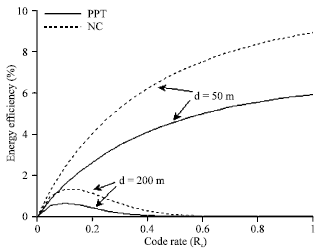
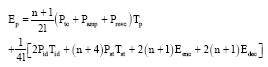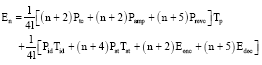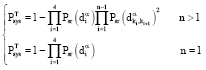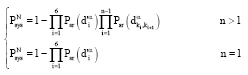Research Article
Research on Energy Efficiency of Wireless Sensor Networks Based on Network Coding
Department of Electronic and Information Engineering, Harbin Institute of Technology, Shenzhen Graduate School, Shenzhen, China
Qinyu Zhang
Department of Electronic and Information Engineering, Harbin Institute of Technology, Shenzhen Graduate School, Shenzhen, China