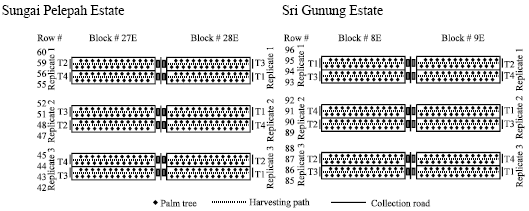
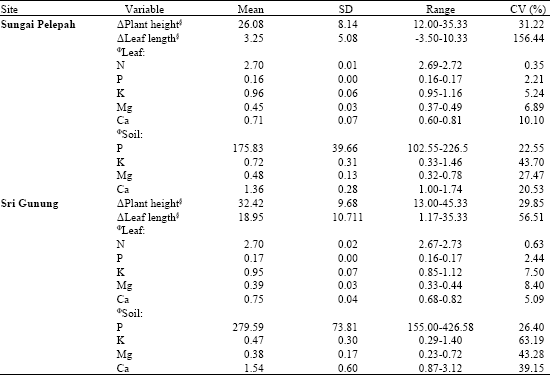
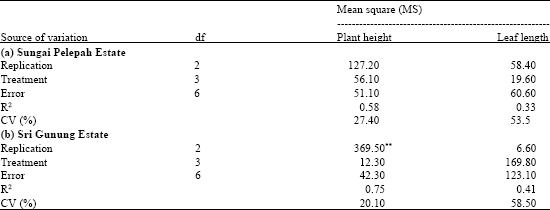
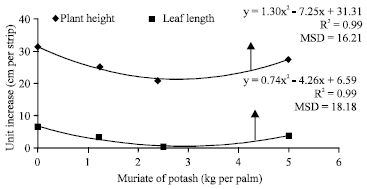
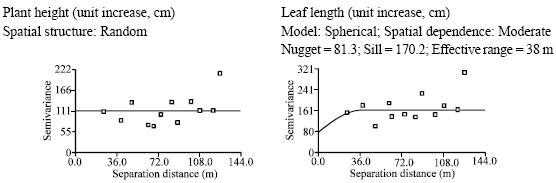
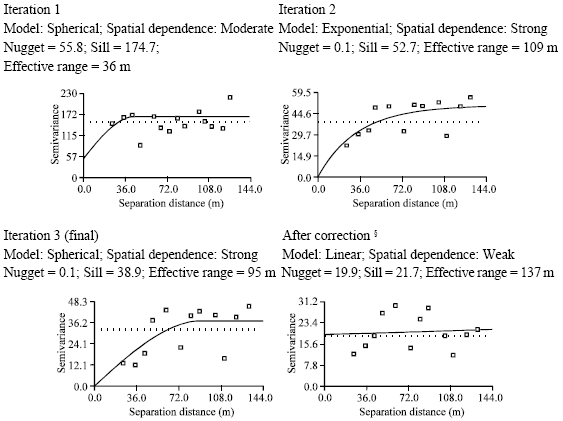
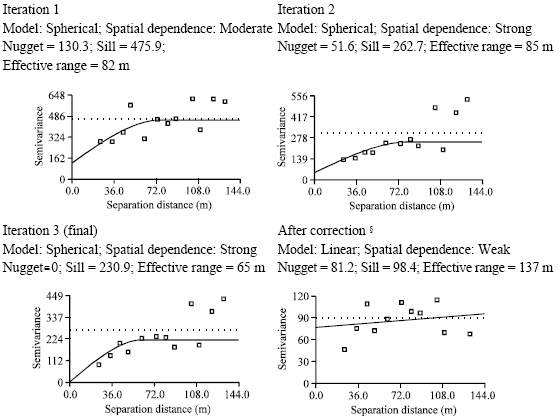
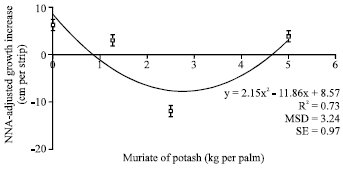
Research Article
Accounting for Spatial Variability in a Short-Term Fertilizer Trial for Oil Palm
Department of Agriculture Technology, Faculty of Agriculture, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
D. J. Mulla
Department of Soil, Water and Climate, University of Minnesota, 439 Borlaug Hall, 1991 Upper Buford Circle, St. Paul, 551 USA
P. C. Robert
(Deceased); Formerly Department of Soil, Water and Climate, Precision Agriculture Center, University of Minnesota, 439 Borlaug Hall, 1 991 Upper Buford Circle: St. Paul, 55108, USA
D. L. Allan
Department of Soil, Water and Climate, University of Minnesota, 439 Borlaug Hall, 1991 Upper Buford Circle, St. Paul, 551 USA