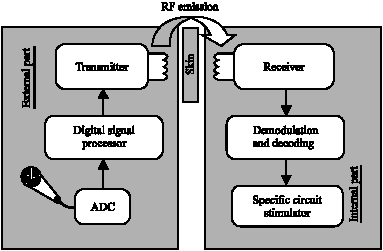
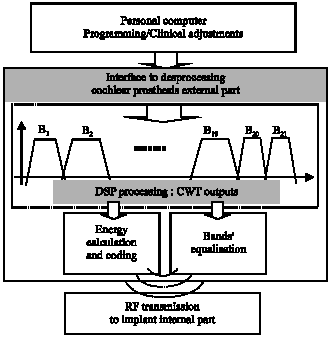
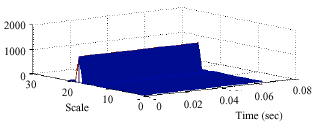
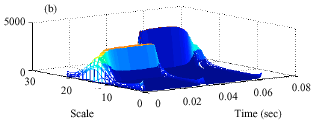
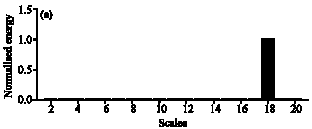
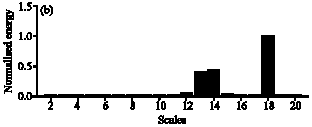
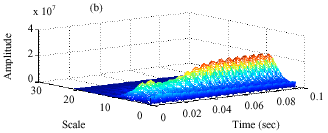
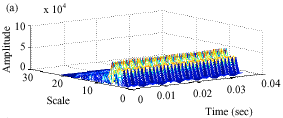
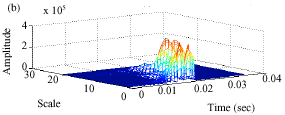
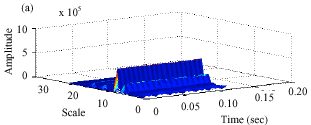
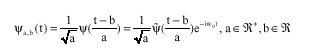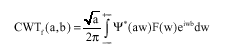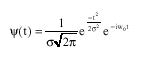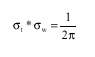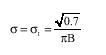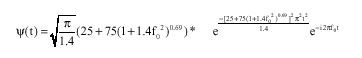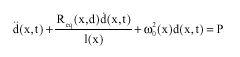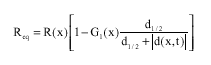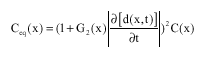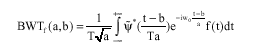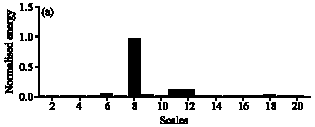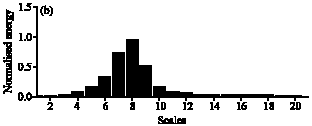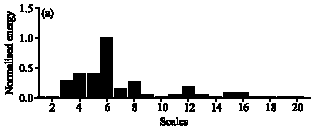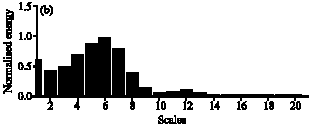Research Article
Bionic Wavelet Transform Based on Speech Processing Dedicated to a Fully Programmable Stimulation Strategy for Cochlear Prostheses
Information Technology and Medical Electronics, LETI, ENIS, University of Sfax, Tunisia
Fathi Kallel
Information Technology and Medical Electronics, LETI, ENIS, University of Sfax, Tunisia
Mounir Samet
Information Technology and Medical Electronics, LETI, ENIS, University of Sfax, Tunisia
Ahmed Ben Hamida
Information Technology and Medical Electronics, LETI, ENIS, University of Sfax, Tunisia