INTRODUCTION

Semi Solid Metallurgy (SSM) is a very trendy near-net-shape manufacturing process. It is of growing industrial significance and the high level of excitement and optimism that pervades the subject is reflected by the large number of publications, the series of conferences and workshops held on the subject.

Whatever, the route employed for SSM, several advantages of the process are clear (Flemings, 2000; Adedayo, 2011a, b). SSM employs reduced temperature when compared to the casting of superheated melts. The generally accepted advantages of hardware performance and energy economy, achieved due to reduced operating temperatures are universally positive for all alloys (Czerwinski, 2008) and includes the following: lower energy consumption, no handling of liquid metal, longer die life, better yield from the raw material due to lower oxidation and evaporation, and fewer other losses related to melt overheating.

Although, SSM is already a viable manufacturing method, it is still under intensive development and critical breakthroughs are still much expected (Czerwinski, 2008). The production of SSM feedstock is of considerable interest and current research effort is concentrated on production of feedstock alloys where the primary phase in the microstructure consists of globularized particles (Reisi and Niroumand, 2008; Paes et al., 2006; Margarido and Robert, 2003). In general, microstructure affects materials properties (Araoyinbo et al., 2010; Omotoso and Ogunsile, 2010; Abdi et al., 2009; Omotosho et al., 2012; Abdullah et al., 2009).

Aside from the major efforts that will certainly take place in overall process development (Flemings, 2000), the Toyota Emeritus Professor of Materials Science and Engineering at Masachuesset Institute of Technology (MIT) identifies some key research directions as the path forward for SSM. Foremost of the key research directions is formulation of better understanding of the mechanism where by the desired SSM microstructure is formed. Also, the development and full application of mathematical models relevant to SSM would be a very vital tool in this quest. Recently, many publications have established the potentials of mathematical models to describe the hydrodynamic characteristics of two phase systems (Kwaire et al., 2010; Abdul-Bari and Yunus, 2009).

In this present study, theoretical expositions are made on some important features of evolution of required microstructure of the SSM component. The understanding of the theories of evolution of required microstructure is vital and useful for SSM process designs and other engineering applications. This will also provide insight on fundamentals for achieving the much expected critical breakthroughs in SSM.

METHODS FOR PRODUCING GLOBULAR CRYSTALS

Under conventional solidification conditions, dendritic microstrutres result (Browne et al., 2003). This process is well discussed in literatures (Kurz and Fisher, 1998; Rajput, 2006). The process of producing globular crystals in metallic alloys which is suitable for SSM was commonly believed to rely upon the fragmentation of the secondary dendrite arms during solidification (Browne et al., 2003; Doherty et al., 1984). A number of technologies have been developed over the last three decades, mainly in a laboratory environment, to take advantage of the unique behavior of semi-solid slurries to produce globular crystals. All the technologies can be divided into two fundamentally different basic routes: thixo-processing and rheo-processing. There are also hybrids that combine features of both routes.

The thixo-route involves two stages: first, billet preparation and, second, billet re-heating and isothermal holding within the mushy zone of the alloy. The crystals which form in the process of conventional solidification of a metal have structures which are dendritic, lamellar or fibrous, needle type (acicular) or globular, depending on the rate of cooling and the type and amount of admixtures or impurities (intermetallics) in the melt (Rajput, 2006). Perfect crystals of proper external shape can be obtained only if crystallization develops under condition when the degree of super cooling is very slight and the metal has a very high purity (Rajput, 2006). In great majority of cases, branched or tree-like crystals are obtained which are called dendrites. Figure 1 shows steps in the formation of a dendritic crystal.

A crystal nucleus forms as shown in (a) and then proceeds to send out shoots or axis of solidification as shown in Fig. 1b-d forming the skeleton of a crystal. Atoms then attach themselves to the axes of the growing crystal from the melt in progressive layers (layers 1, 2, 3, 4 and 5 as shown in Fig. 1e), finally filling up these axes, and thus forming a completed solid crystal.

However, during billet re-heating thixo-processing of the metallic alloy there is partial melting of the structures in the alloy. These may be any of the various compounds found in the alloy. Constituents with low melting points melt into liquid. Also, as the temperature rises, there is break-up of the primary and secondary axis into smaller unit and random re-orientation of the break-up network. Due to high diffusion rates in the mushy zone, atoms of the melted constituents diffuse from the liquid phase and joined up with the existing solid crystals. This phenomenon leads to evolution of new structure which is globular. This process is shown in Fig. 2.

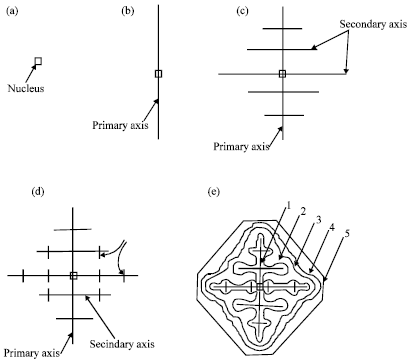Fig. 1:	Formation of dendritic crystals (Rajput, 2006)

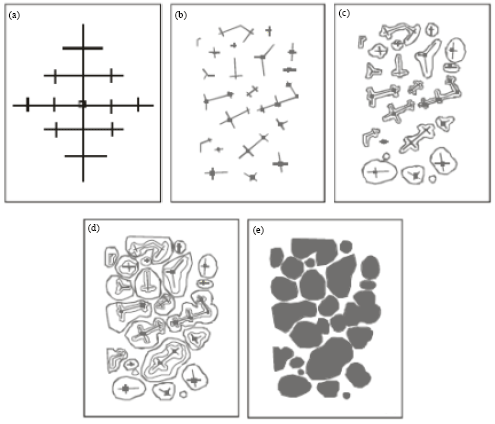Fig. 2:	Development of globular structure (a) Dendritic structure formed during solidification in a casting (b) Breakdown of dendritic network to form new nuclei during semi solid isothermal heating, (c), (d) and (e) The process of emergence of globular structure (Adedayo, 2011a)

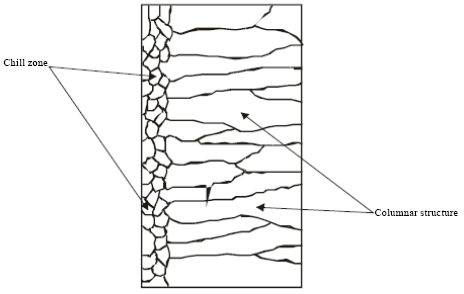Fig. 3:	Sketch of chill zone and columnar structure in conventional casting

TEMPERATURE AND GLOBULAR MORPHOLOGY

In conventional castings, the material in the interior of the ingot cools more slowly and solidification takes place at a higher temperature. Usually, some of the grains near the surface simply grow inwards as heat flows outwards. The resulting structure is columnar (illustrated in Fig. 3). The columnar grains are not randomly oriented but rather have their directions of most rapid growth normal to the mould walls, which is the direction of heat withdrawal. In general, crystals grow in certain directions depending on some factors such as direction of heat flow and presence of impurities.

The direction of heat flow is a function of the temperature field. In mathematical physics, the temperature field is the totality of temperature values at a given point in time for all points of the space considered in which heat transfer process takes place. During solidification, the temperature at various points change with time and heat propagates from places at a higher temperature to places at lower temperature. It follows that during solidification, there is variation of temperature both in space and time.

INFLUENCE OF FURNACE DESIGN ON SEMI SOLID MICROSTRUCTURE

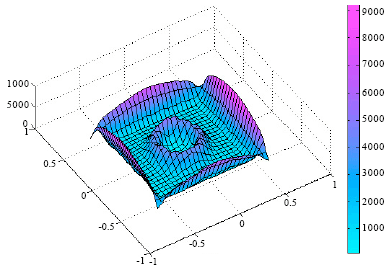
Heat flow patterns in furnaces have been studied using Finite Element (FE) analysis by Oluwole et al. (2009). This study revealed that the design of a furnace has effects on the heat flow characteristics of the furnace. The long term stability of the furnace was also found to be dependent on the design. The thermal stability of the furnace determines the temperature profile within the furnace per time. Consider Fig. 4 and 5, these show that the furnace design has significant effects on the temperature gradients in the furnace.

For alloy materials, when the grain boundary grooving occurs such that the boundary intersects the liquid-solid interface, the curvature in the neighborhood of the groove is determined by the requirement that (Fleming, 1974):

(1)

where, T* is the liquid-solid interface temperature, G is the thermal gradient and ΔX is the distance back from the isotherm at T_m, the equilibrium melting point of the alloy material (the liquidus temperature).

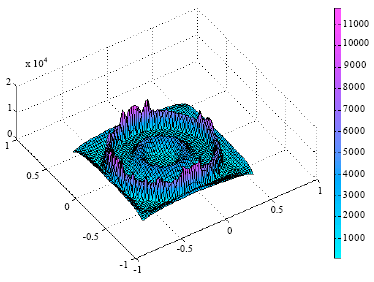Fig. 4:	A 3-D presentation of a salt bath furnace showing temperature gradients during heat transfer in the furnace (A high temperature gradient was observed in the air gap insulation) (Oluwole et al., 2009)

Fig. 5:	A 3-D salt bath furnace without air-gap spacing insulation within refractory lining showing temperature gradients during heat transfer in the furnace (A high temperature gradient was observed concentrated in the glass wool fibre segment) (Oluwole et al., 2009)

But also:

(2)

(3)

where, ΔG_L and ΔG_s are the changes in free energies of liquid and solid, respectively. Vs is the volume of the solid, λ is the surface curvature in the groove neighborhood, T_r is the decrease in equilibrium melting point, σ is the surface energy of the interface. Assuming that ó is isotropic and does not change as surface area changes, at equilibrium (Fleming, 1974):

(4)

It follows that:

(5)

(6)

(7)

(8)

(9)

(10)

But:

(11)

(12)

(13)

But the curvature λ at a point is described as the limit (provided it exists) of the average curvature λ_av (Fig. 6) of an arc as the terminal point of the arc tends to its initial point (Bermant and Aramanovich, 1989). For arc M₀ M₁, as the terminal point of the arc M₁ tends to its initial point M₀:

(14)

where, φ is the angle of contingence of the arc (in radians).

Fig. 6:	Geometric description of relationship between r, φ and curvature (λ)

So:

(15)

Thus:

(16)

Therefore:

(17)

Then:

(18)

The thermal gradient G is dependent on the stability of the furnace (Oluwole et al., 2009). If the temperature field of the system is transient i.e.:

(19)

where, x, y, z are point coordinates, t is time. The thermal gradient G will be dependent on time and the value of r will vary with time. Transient temperature fields are experienced during heating and cooling of a system.

During isothermal heating, the temperature field is steady i.e.:

(20)

Temperature gradient G will be essentially constant and independent of time. This gives an essentially constant value for r. This results in a spheroidal morphology. This shows that the ability of the heat treatment furnace to maintain an efficient steady-state will affect the morphology of the evolving crystal. Also, value of G (whether G<0 or G>0) will affect the concavity or convexity of the resulting microstructure.

INTERMETALLICS AND GLOBULAR MORPHOLOGY

The relationship between curvature λ and surface energy σ of the interface can be expressed by Eq. 12, as:

(12)

However, for a multi-component surface, the resultant surface energy will depend on crystallographic orientation and the surface energies of the constituent components. The resultant surface energy may be evaluated using Cassie equation (Adedayo et al., 2010; Adedayo, 2010):

(21)

i.e.:

(22)

where, Cosθ is proportional to the resultant surface energy, f_i is the fraction of component i and θ_i is the contact angle of component i. Therefore:

(23)

Therefore:

(24)

This shows the dependence of r and hence λ on:

(25)

FORMULATION FOR PREDICTING COMPOSITION OF A GLOBULE

SSM is feasible only with alloys because there exists a MUSHY zone in their phase diagram. Generally, alloys are systems containing two or more different elements. In the slurry zone the constituents of alloys may react to form intermetallics and eutectics. Actually, the reacting species in the alloys are in a balance with the products of reaction because a sort of equilibra is established within the system. Also, in the mushy (slurry) zone, there is a balance between the solid and the liquid phases of the alloy present. This leads to solute redistribution between the solid and the liquid and thus varied compositions of the solid and the liquid. At temperature T, a general material balance (conserving solute atoms) is written:

(26)

where, f_s and f_L are weight fractions of solid and liquid, respectively. C_s and C_L are the solid compositions, respectively. C₀ is the initial composition of the alloy. At temperature T, solid of composition Cs is freezing from liquid of composition C_L. A quantitative expression is easily obtained by equating the solute rejected when a small amount of solid forms with the resulting solute increase in the liquid. This balance is:

(27)

If:

(28)

where, k is defined as the partition ratio then:

(29)

(30)

Therefore:

(31)

Substituting the equilibrium partition ratio and integrating from C_s = kC₀ at f_s = 0, the composition of the globule at the liquid-solid interface Cs as a function of fraction of solid is given as:

(32)

(33)

(34)

Integrating from 0 to fs and from kC₀ to Cs:

(35)

Substituting 0 and fs for values of fs and kC₀ and Cs for values of Cs:

(36)

(37)

(38)

Therefore:

(39)

Or in terms of liquid composition and fraction liquid:

(40)

TEMPERATURE AND GLOBULE FRACTION

In metal alloys and other alloys where the liquid-solid interface is close to equilibrium, liquid composition within any given interdendritic space is almost uniform and close to the liquidus line of the phase diagram. This assumes a constant liquidus slope M_L (Fig. 7):

where, T is the temperature of the volume element, T_m is the melting point of the pure solvent metal. Thus:

(41)

But:

Where:

(42)

Therefore:

(43)

(44)

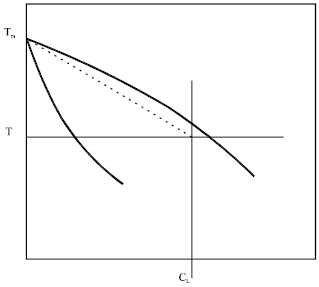Fig. 7:	Model of the liquid-solid region

Taking logarithm of both sides:

(45)

(46)

(47)

Globule fraction (solid fraction) is given as:

(48)

(49)

(50)

(51)

The formulation for predicting fraction of a globule is given as: