Research Article
Bayesian Using Extension of Jeffreys Estimator of Weibull Distribution Based on Type-I and II Cnsored Data
Department of Mathematics, Faculty of Arts and Science in Qilwah, Al-Baha University, Baha, Saudi Arabia
The Weibull distribution has the widest variety of many applications in different areas, including lifetime testing, reliability theory and others. Sinha (1986) estimated the scale and shape parameters of Weibull distribution by MLE and Bayesian methods. Smith and Naylor (1987) developed the maximum likelihood and Bayesian approach and compared them using the Weibull distribution. Sun (1997) estimated the two parameters of Weibull distribution where he compared Jeffreys prior with that of the reference prior under Bayesian methods. Hossain and Zimmer (2003) estimated the parameters of Weibull distribution using complete and censored samples by MLE and least squares method. Singh et al. (2005) obtained Bayesian and MLE for Exponentiated Weibull distribution based type-II censoring. Soliman et al. (2006) estimated Weibull distribution by using MLE and Bayesian estimation following by estimated the hazard and reliability functions. Kantar and Senoglu (2008) reported their findings on the comparative study for the location and scale parameters of the Weibull distribution with a given shape parameter. Kundu and Howlader (2010) obtained Bayesian inference and prediction of the inverse Weibull distribution based type-II censored data. Pandey et al. (2011) compared Bayesian estimation and MLE of the scale parameter in Weibull distribution with known shape.
The objective of this study is to estimate the scale parameter, survival and hazard functions of the Weibull distribution based on type-I and II censored data by using Bayesian approach and compared to MLE using Mean Square Error (MSE) to determine the better estimator under several conditions.
Maximum likelihood estimation of Weibull censored data: Concept of maximum likelihood estimation on Weibull distribution with censored data was introduced here. Let (x1,…, xn) be the set of n random lifetime from Weibull distribution with parameters λ and α.
The probability density function of Weibull distribution is:
where, the Cumulative Distribution Function (CDF) of the Weibull distribution is given as:
with λ as the scale parameter and α the shape parameter of the Weibull distribution.
| • | Maximum likelihood estimation based on type-I censored data: The likelihood function as in the study of Klein and Moeschberger (2003) is: |
| (1) |
| where, δi is 1 for failure and δi is 0 for censored observation and S(.) is the survival function. |
| The logarithm of the likelihood function can be expressed as follows: |
| (2) |
To obtain the equations for the unknown parameters, we differentiate Eq. 2 partially with respect to the parameters λ and α and equal it to zero. The resulting equations are given as follows:
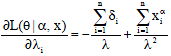 | (3) |
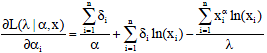 | (4) |
Let Eq. 3 equals to zero, then the maximum likelihood estimator for the scale parameter of Weibull distribution is:
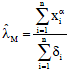 | (5) |
The shape parameter cannot be solved analytically and for that we use the Newton Raphson method to find the numerical solution following (Hossain and Zimmer, 2003).
The estimate of the survival function for Maximum Likelihood Estimation of Weibull distribution is:
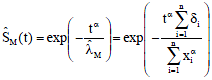 | (6) |
The estimate of the hazard function of Weibull distribution given shape by Maximum Likelihood Estimation is as follows:
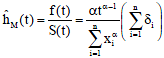 | (7) |
| • | Maximum likelihood estimation based on type-II censored data: The likelihood function is: |
| (8) |
The logarithm of the likelihood function can be expressed as follows:
 | (9) |
To obtain the equations for the unknown parameters, Eq. 9 is differentiated partially with respect to the parameters λ and α and equal it to zero. The resulting equations are given, respectively as:
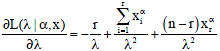 | (10) |
 | (11) |
Let Eq. 10 equals to zero, then the maximum likelihood estimator for the scale parameter of Weibull distribution is:
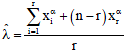 | (12) |
The shape parameter cannot be solved analytically and for that we employed Newton Raphson method.
The estimate of the survival function for MLE based type-II censored data:
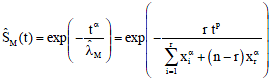 | (13) |
The estimate of the hazard function of Weibull based type-II censored data:
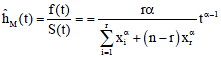 | (14) |
Bayesian estimation of weibull based on type-I censored data: The Bayesian estimator with Jeffreys prior is described here, where Jeffreys prior is the square root of the determinant of the Fisher information matrix:
Then the Jeffreys prior is:
| (15) |
where, k is a constant.
The posterior probability density function of λ given the data (t1,…, tn) is obtained by dividing the joint probability density function with the marginal density function (Ahmed et al., 2012):
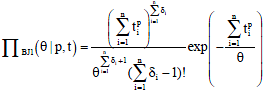 | (16) |
With this, the Bayesian estimates for the scale parameter of Weibull distribution under squared error loss function are given as:
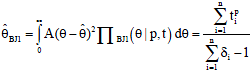 | (17) |
The estimator for survival function of Weibull distribution given shape by Bayesian using Jeffreys prior obtained as:
 | (18) |
The estimator for hazard function of Weibull distribution given shape by Bayesian using Jeffreys prior obtained as:
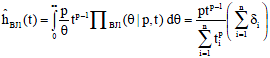 | (19) |
| • | Extension of Jeffreys prior information based on type-I censored data: Extension of Jeffreys prior information is the Fisher information with the variable c where, c is a positive real number as: |
| (20) |
The posterior probability density function of λ based on type-I censored data is:
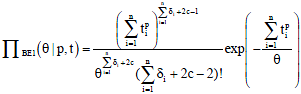 | (21) |
With this, the Bayesian for extension of Jeffreys prior estimates the scale parameter of Weibull distribution under squared error loss function are given as:
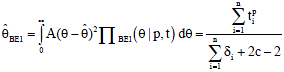 | (22) |
The estimator for survival function of Weibull distribution given shape by Bayesian using extension of Jeffreys obtained as:
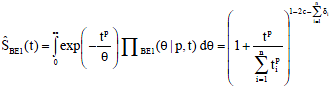 | (23) |
The estimator for hazard function of Weibull distribution by Bayesian using extension of Jeffreys obtained as:
 | (24) |
Bayesian estimation of Weibull based on type-II censored data: The posterior probability density function of λ based on type-II censored data:
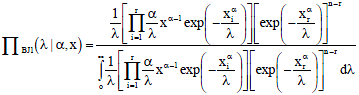 | (25) |
With this, the Bayesian estimate for the scale parameter of Weibull distribution under squared error loss function is given as:
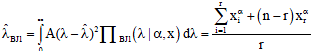 | (26) |
The estimate of the survival function of Weibull distribution given shape by Bayesian using Jeffreys prior is:
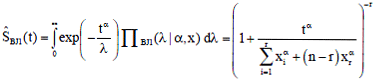 | (27) |
The estimate of the hazard function of Weibull distribution based on type-II censored data by Bayesian using Jeffreys prior is obtained by:
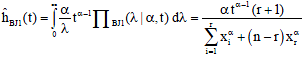 | (28) |
The posterior probability density function of λ based on type-II censored data:
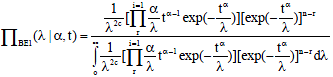 | (29) |
With this, Bayesian with extension of Jeffreys prior estimate of the scale parameter of Weibull distribution based on type-II censored data are given as:
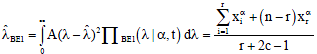 | (30) |
The estimate of the survival function of Weibull distribution given shape by Bayesian using extension of Jeffreys prior is obtained as:
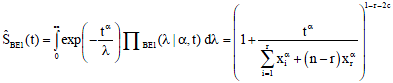 | (31) |
The estimate of the hazard function of Weibull distribution by Bayesian using extension of Jeffreys prior based on type-II censored data obtained as:
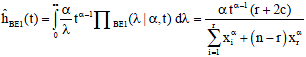 | (32) |
Simulation study: To assess the performance of the maximum likelihood and Bayesian estimation based on type-I and II censored data to estimate the scale parameter follow by estimate survival and hazard functions. The Mean Squared Errors (MSE) was calculated using 10,000 replications for sample size n = 25, 50 and 100 of Weibull distribution with type-I and II censored data for different value of parameters were the scale parameter λ = 0.8 and 1.2, the shape parameter α = 0.5 and 1.5 and the two values of Jeffreys extension were c = 0.4 and 1.4, the considered values of parameters and extension of Jeffreys are meant for illustration only and other values can be taken for generating the samples from Weibull distribution.
Four values of the estimators which are MLE, Bayesian using Jeffreys prior (BJ), extension of Jeffreys prior with c = 0.4 (BE(c = 0.4)) and extension of Jeffreys prior with c = 1.4 (BE(c = 1.4)) are shown in each column for each size.
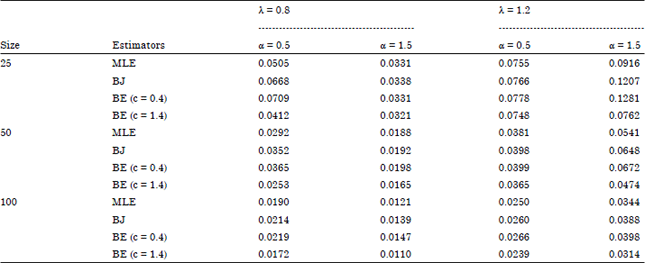
Table 1 contains the estimate of the scale parameter of Weibull distribution based type-I censored data with maximum likelihood, Bayesian using Jeffreys prior and extension of Jeffreys prior information.
From Table 2 the results show that when c = 0.4, the maximum likelihood is better compared to the others with respect to the MSE of scale parameter. On the other hand, when c = 1.4, extension of Jeffrey is better compared to the others (Ahmed et al., 2011). This implies that, as the value of extension of Jeffreys prior is kept below one, it exerts very minimal influence on the posterior distribution but as it increases to at least above one, the influence becomes significant on the posterior distribution from which Bayesian inference is drawn to give a very small mean squared error as compared to maximum likelihood and that of Jeffreys prior.
Table 3 shows the comparison of the survival function with the maximum likelihood is noticed to be better compared to the others when c = 0.4. On the other hand, when c = 1.4, extension of Jeffrey is better compared to the others following Ahmed et al. (2011).
| Table 1: | Estimate λ based type-I censored data |
 | |
| Table 2: | MSE for the scale parameter of Weibull based type-I censored data |
 | |
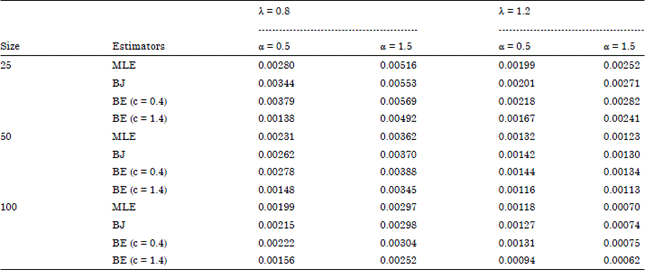
| Table 3: | MSE for the survival function of Weibull based type- I censored data |
 | |
| Table 4: | MSE for the hazard function of Weibull based type-I censored data |
 | |
As shown in Table 4 the hazard function estimates based on type-I censoring data was compared. The results show that when c = 0.4, the maximum likelihood is better compared to the others. Nevertheless, when c = 1.4, extension of Jeffrey has the smaller mean squared error as compared to others.
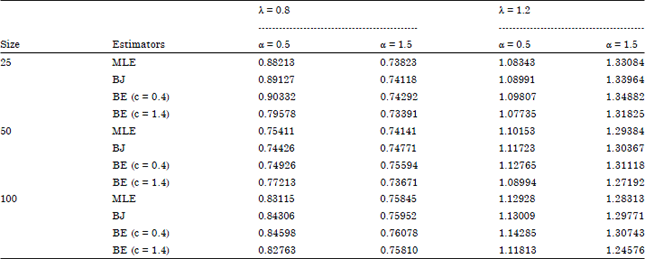
Table 5 estimates the scale parameter of Weibull distribution based type-II censored data with Maximum likelihood, Bayesian using Jeffreys prior and extension of Jeffreys prior.
Table 6 observed that, the mean squared errors of the Bayes estimator based type-II censored data under the extension of Jeffreys prior (c = 0.4) is the best estimator of the scale parameter for all the cases.
The survival function as indicated in Table 7 show that, the Bayesian using extension of Jeffreys based on type-II censored data is the best for all cases.
Table 8 show that, extension of Jeffreys prior based on type-II censored data is the best estimation.
| Table 5: | Estimate λ based type-II censored data |
 | |
| Table 6: | MSE for the scale parameter of Weibull based type-II censored data |
 | |
| Table 7: | MSE for the survival function of Weibull based type-II censored data |
 | |
| Table 8: | MSE for the hazard function of Weibull based type-II censored data |
 | |
In this study we have considered the Bayesian using extension of Jeffreys prior based on type-I and II censored data. The result show that, the Bayesian using extension of Jeffreys prior based on type-I is better estimator for all estimated of the scale parameter and the survival and hazard functions when the value of extension of Jeffreys is 1.4. On the other hand, the maximum likelihood method is better than others when the value of extension of Jeffreys is 0.4. The Bayesian using extension of Jeffreys prior based on type-II censored data is the best estimation compared to the other estimation.