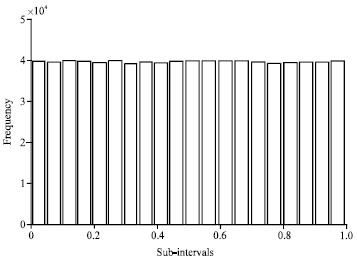
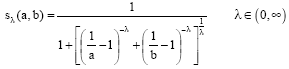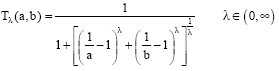Research Article
Fuzzy Cellular Automata Based Random Numbers Generation
Department of Computer, Bojnourd Branch, Islamic Azad University, Bojnourd, Iran
Azam S. Zavar Mousavi
Department of Computer, Bojnourd Branch, Islamic Azad University, Bojnourd, Iran
Ehsan Shahamatnia
Department of Electrical and Computer Engineering, UNINOVA, FCT, Universidade Nova de Lisboa, Caparica, Portugal