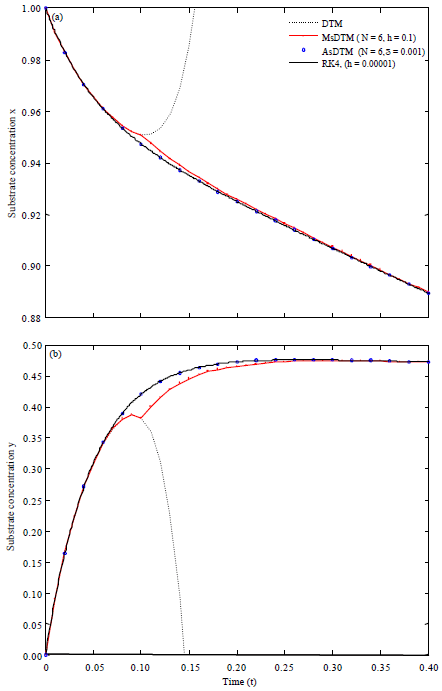
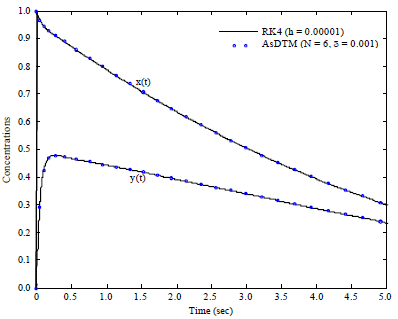
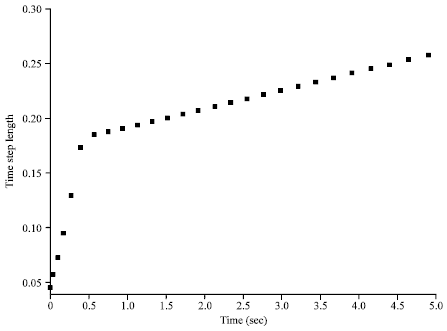
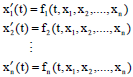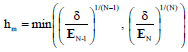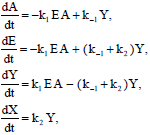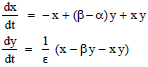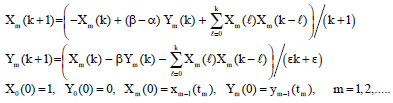Research Article
An Adaptive Step-Size Taylor Series Based Method and Application to Nonlinear Biochemical Reaction Model
Department of Mathematics, College of Sciences and Humanities, Salman Bin Abdulaziz University, P.O. Box 83, Alkharj, 11942, Saudi Arabia