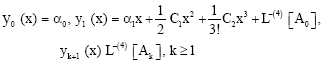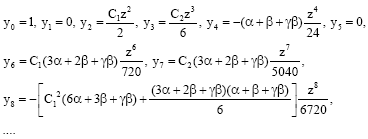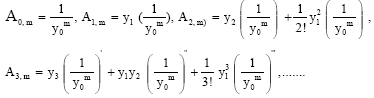Research Article
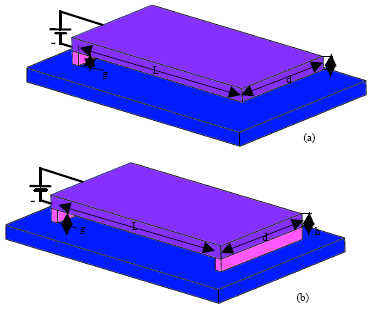
Efficiency of Modified Adomian Decomposition for Simulating the Instability of Nano-electromechanical Switches: Comparison with the Conventional Decomposition Method
Mechanical Engineering Group, Naein Branch, Islamic Azad University, Naein, Iran
M. Abadyan
Mechanical Engineering Group, Shahrekord Branch, Islamic Azad University, Shahrekord, Iran