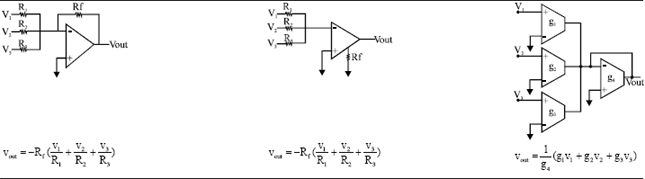
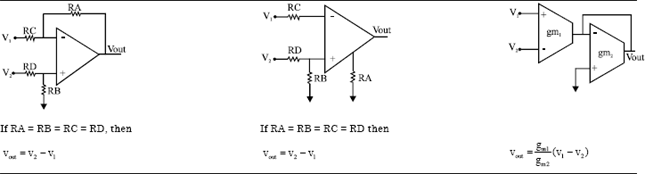
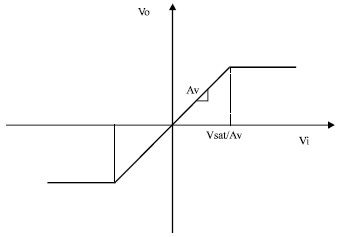
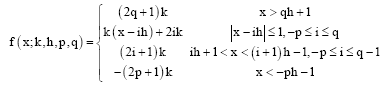Research Article
OpAmp-, CFOA- and OTA-Based Configurations to Design Multi-Scroll Chaotic Oscillators
Universidad Politenica de Puebla, Puebla, 72000, Mexico
W. Campos-Lopez
Universidad Politenica de Puebla, Puebla, 72000, Mexico
E. Tlelo-Cuautle
INAOE, Tonantzintla, 72840, Mexico
C. Sanchez-Lopez
Universidad Autonoma de Tlaxcala, Tlaxcala, 72000, Mexico