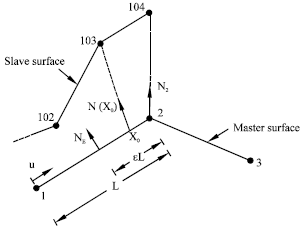
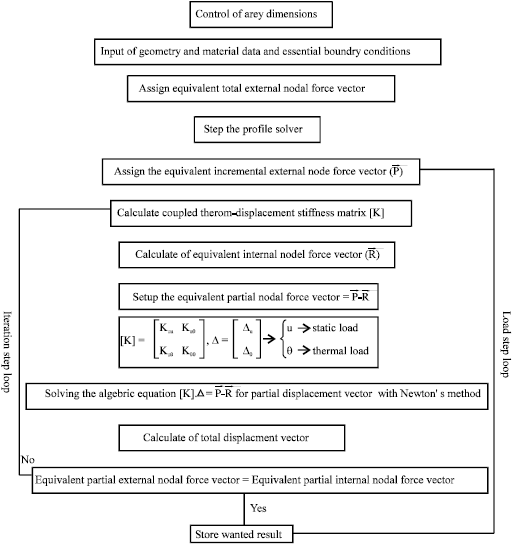
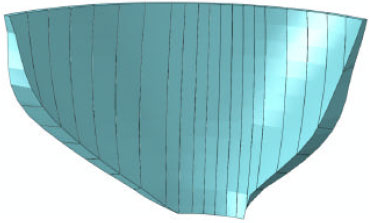
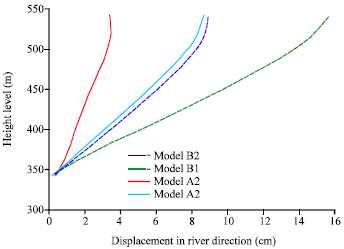
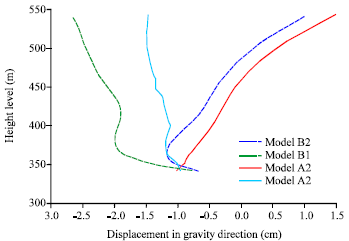
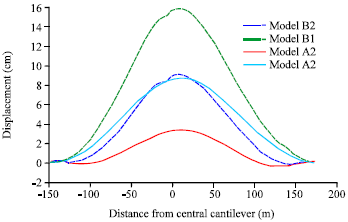
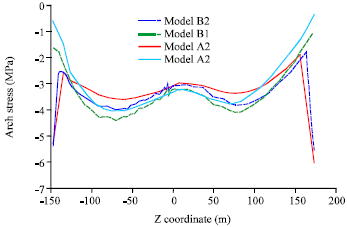
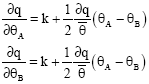Research Article
Effect of Vertical Contraction Joints on Thermo-Static Stability of Karun-1 Arch Dam
Department of Civil Engineering, Faculty of Engineering, Shahid Chamran University, Ahvaz, Iran
A. Khajehdezfuly
Department of Civil Engineering, Faculty of Engineering, Shahid Chamran University, Ahvaz, Iran