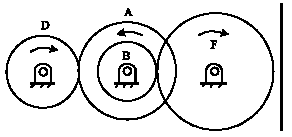
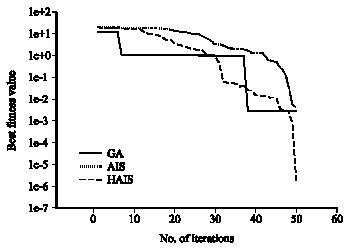
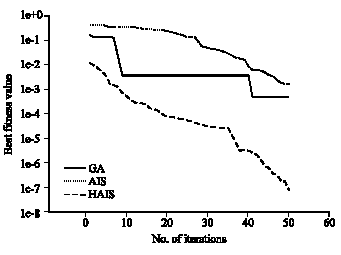
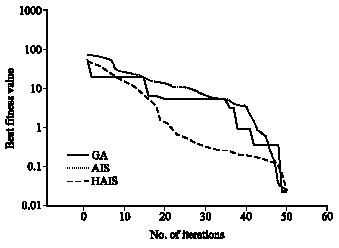
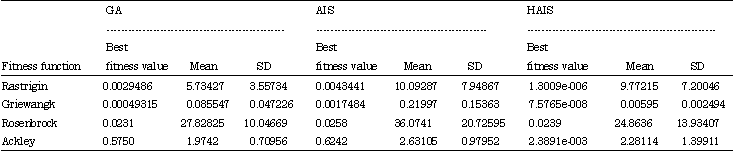
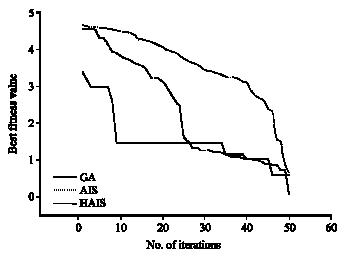
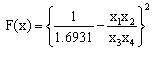Research Article
Particle Swarm based Artificial Immune System for Multimodal Function Optimization and Engineering Application Problem
Faculty of Electronics and Computer Engineering, Universiti Teknikal Malaysia Melaka (UTeM), Hang Tuah Jaya, 76100 Durian Tunggal, Melaka, Malaysia
S.P. Koh
College of Engineering, Universiti Tenaga Nasional (UNITEN), km 7, Kajang-Puchong Road, 43009 Kajang, Selangor Darul Ehsan, Malaysia
S.K. Tiong
College of Engineering, Universiti Tenaga Nasional (UNITEN), km 7, Kajang-Puchong Road, 43009 Kajang, Selangor Darul Ehsan, Malaysia
S.K. Prajindra
College of Engineering, Universiti Tenaga Nasional (UNITEN), km 7, Kajang-Puchong Road, 43009 Kajang, Selangor Darul Ehsan, Malaysia