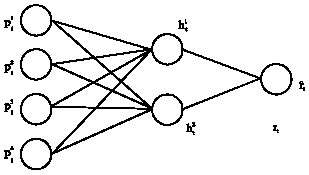
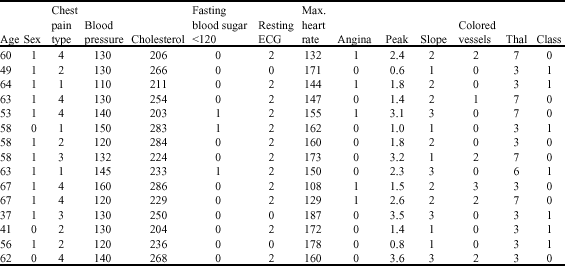
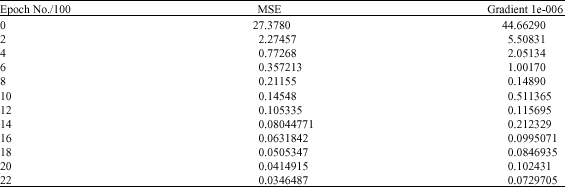
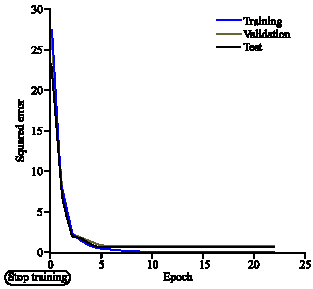
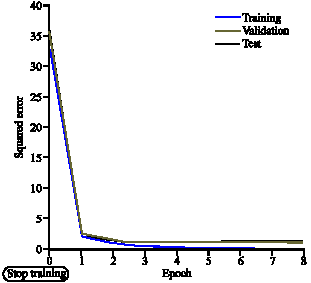
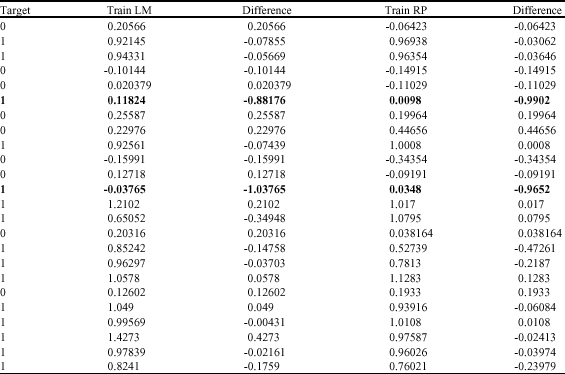
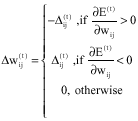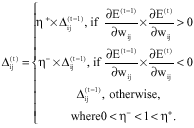Research Article
Artificial Neural Network as a Clinical Decision-Supporting Tool to Predict Cardiovascular Disease
Faculty of Science, University of Mauritius, Réduit, Mauritius
Jayrani Cheeneebash
Faculty of Science, University of Mauritius, Réduit, Mauritius
Ashvin Gopaul
Faculty of Science, University of Mauritius, Réduit, Mauritius
Smita S.D. Goorah
Faculty of Science, University of Mauritius, Réduit, Mauritius