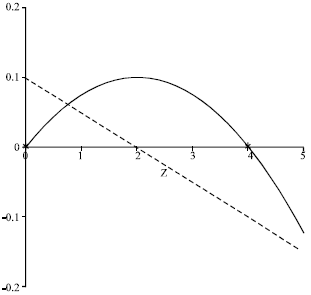
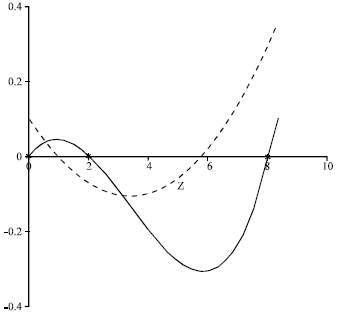
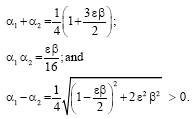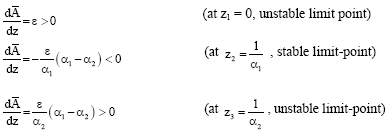Research Article
On the Stable Limit-point of a Modified Van Der Pol Equation
Structural Analysis and Testing Group, Vikram Sarabhai Space Centre, Trivandrurn-695022, India
B. Nageswara Rao
Structural Analysis and Testing Group, Vikram Sarabhai Space Centre, Trivandrurn-695022, India
H.R. Nataraja
Compressor Group, Gas Turbine Research Establishment, C.V. Raman Nagar, Bangalore-560093, India
K.S. Sai
Department of Mathematics, S.V.H. College of Engineering, Machilipatnarn-521002, India