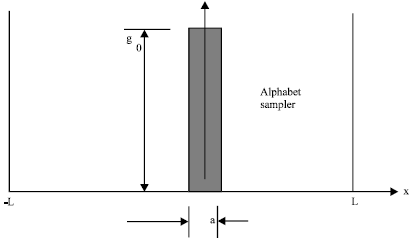
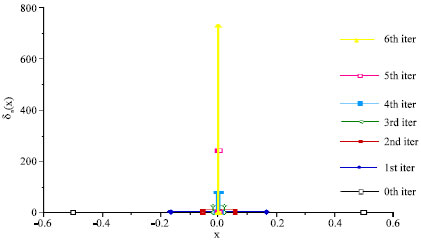
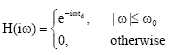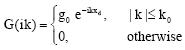Research Article
Transformation of Spoken to Written Forms of (Natural) Languages via Spectral and Pseudo-spectral Methods
University Park Campus, University of Southern California, Los Angeles, CA 90089
Aadel A. Chaudhuri
Stanford University School of Medicine, Stanford, California, 94305