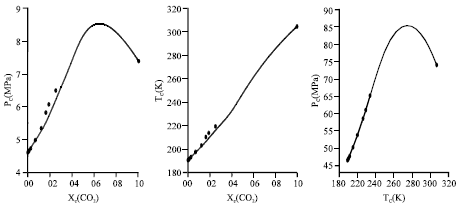
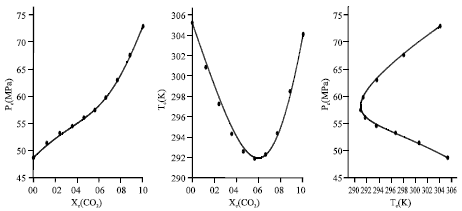
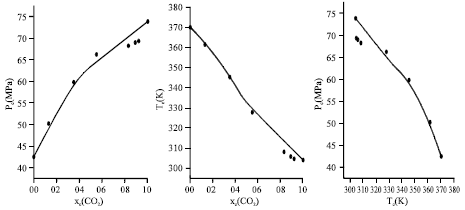
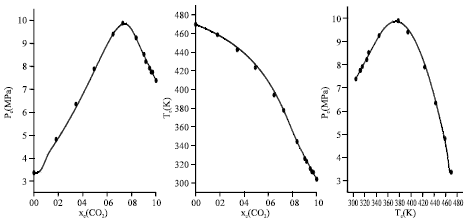
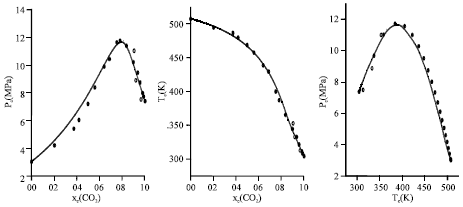
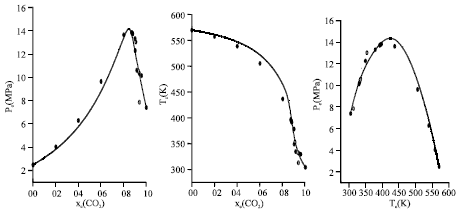
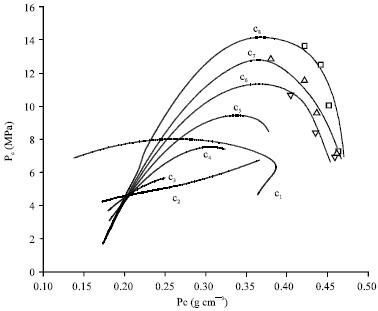
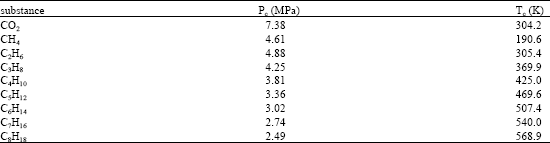
Research Article
Calculation of Critical Curves for Carbon Dioxide+n-Alkane Systems
Department of Chemistry, Tianjin University, Tianjin, 300072, China
Shujun Wang
College of Pharmaceuticals and Biotechnology, Tianjin University, Tianjin, 300072, China
Yiling Tian
Department of Chemistry, Tianjin University, Tianjin, 300072, China
Wei Xu
College of Pharmaceuticals and Biotechnology, Tianjin University, Tianjin, 300072, China