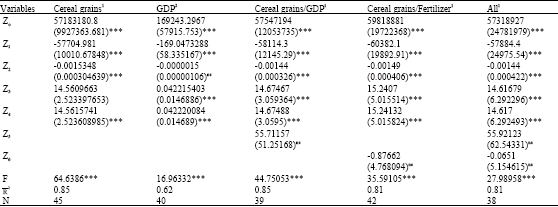
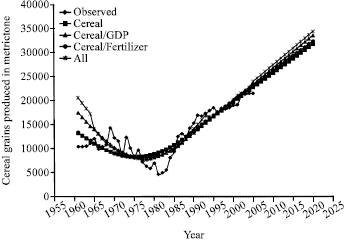
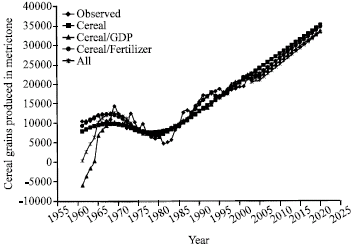
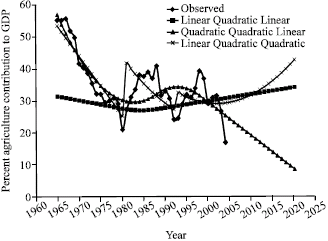
Research Article
Spline Functions: Assessing their Forecasting Consistency with Changes in the Type of Model and Choice of Joint Points
Department of Agricultural Economics and Extension Technology, Federal University of Technology, Minna, Nigeria
E.S. Yisa
Department of Agricultural Economics and Extension Technology, Federal University of Technology, Minna, Nigeria
U.S. Mohammed
Department of Agricultural Economics and Extension Technology, Federal University of Technology, Minna, Nigeria