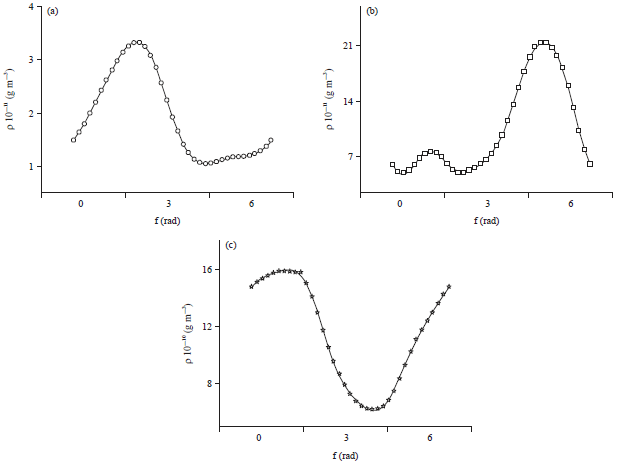
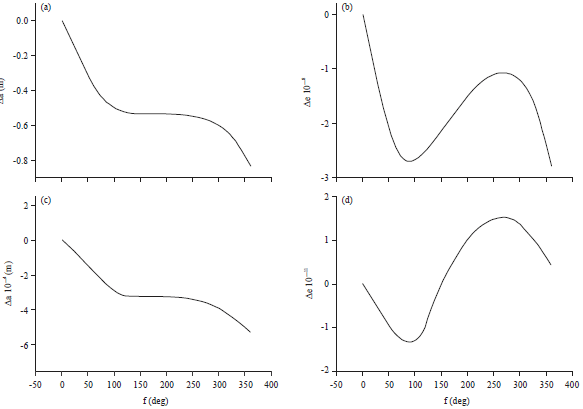
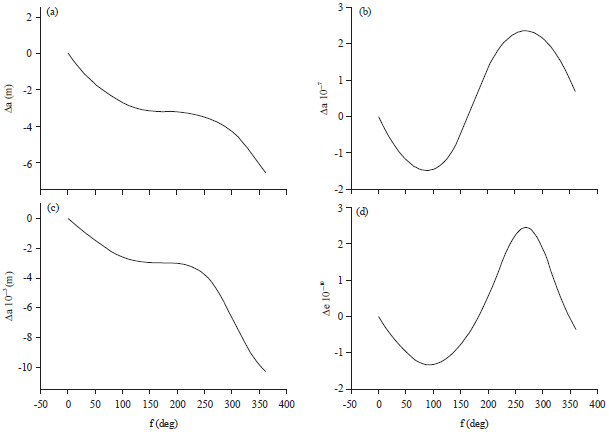
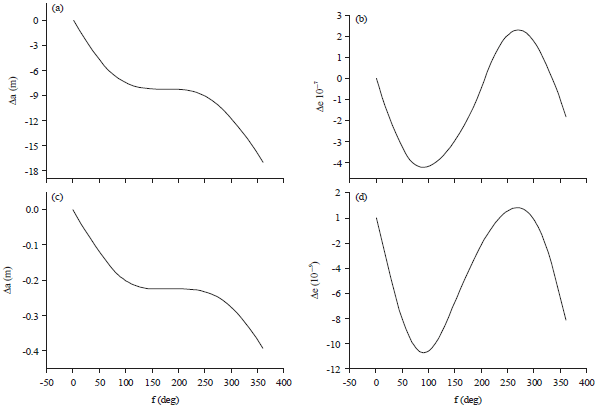
Research Article
Effect of Air Drag Force on Low Earth Orbit Satellites During Maximum and Minimum Solar Activity
National Research Institute of Astronomy and Geophysics (NRIAG), National Research Institute of Astronomy and Geophysics (NRIAG), Elmarsad St., 11421, Helwan, Cairo, Egypt
S.W. Samwel
National Research Institute of Astronomy and Geophysics (NRIAG), National Research Institute of Astronomy and Geophysics (NRIAG), Elmarsad St., 11421, Helwan, Cairo, Egypt