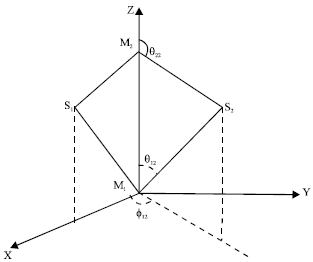
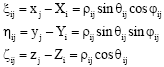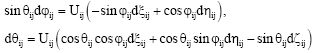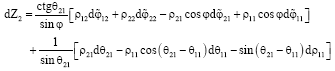Research Article
The Accuracy of the Distance Between Two Stations using Synchronous Optical Observations of the Artificial Satellites in Combination with One Laser Measurement
National Research Institute of Astronomy and Geophysics (NRIAG), Helwan, Cairo, Egypt