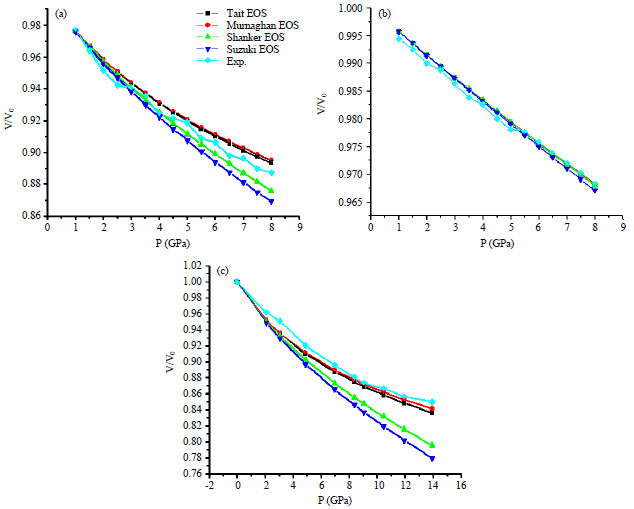
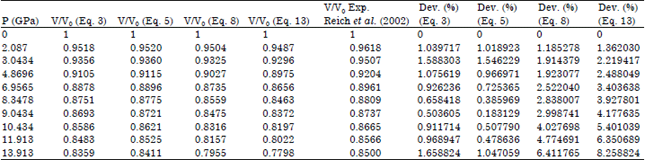
Research Article
Validity of High Pressure Isothermal Equation of State for Carbon Nanotubes
Department of Applied Science, Sherwood College of Engineering Research and Technology, Barabanki, Uttar Pradesh, India
H.K. Rai
Solid State Chemistry Laboratory, Department of Chemistry, Sri J.N. (PG) College, Lucknow, India
B.K. Pandey
Department of Applied Science, MMM University of Technology, Gorakhpur, Uttar Paradesh, India
Abhay P. Srivastava
Department of Applied Science, MMM University of Technology, Gorakhpur, Uttar Paradesh, India
C.K. Singh
Department of Applied Science, MMM University of Technology, Gorakhpur, Uttar Paradesh, India