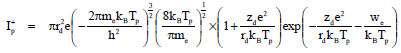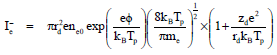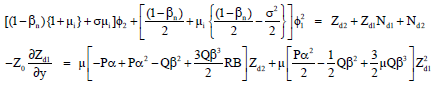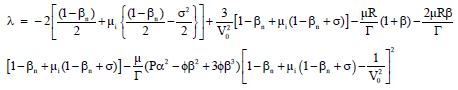Research Article
Effect of Nonthermal Electron on Dust-acoustic Shock Waves in Dusty Plasma
Theoretical Physics Group, Department of Physics, University of Uyo, Uyo, Nigeria
Akpan N. Ikot
Theoretical Physics Group, Department of Physics, University of Uyo, Uyo, Nigeria