Research Article
Critical Phenomena in Bilayer Biomembranes
Polymer Physics And Critical Phenomena Laboratory,Faculty of Sciences Ben M�sik, P.O. Box 7955, Casablanca, Morocco
The cell membranes play a capital role in life, because they separate the cell from the surrounding environment and compartments inside the cell, in order to protect important processes and specific events.
Nowadays, it is largely recognized that the biological membranes present as a lipid bilayer composed of two adjacent leaflets (Lipowsky and Sasckmann, 1995; Benhamou, 2008; Wolfe, 1993; Alberts et al., 1994), which are formed by amphiphile molecules possessing hydrophilic polar-heads pointing out and hydrophobic fatty acyls chains forming the core. The majority of lipid molecules are phospholipids (Lipowsky and Sasckmann, 1995; Benhamou, 2008; Wolfe, 1993; Alberts et al., 1994). These have a polar-head group and two non-polar hydrocarbon tails, of which the length is of the order of 5 nm. The polar-head is attached by glycerol to two fatty acid chains. One of these is a saturated straight fatty acid tail, while the other possesses a kink in the tail due to a cis double bound. Of course, this kink influences packing and lateral movement of host lipid molecules.
Bilayer membranes include another type of lipid that is cholesterol (Lipowsky and Sasckmann, 1995; Benhamou, 2008; Wolfe, 1993; Alberts et al., 1994). For example, plasma membranes contain one cholesterol per phospholipid molecule. This molecule lipid is amphiphile and has a steroid structure. Its size is small in comparison to phospholipids. Within the bilayer, the cholesterol molecules have the same orientation as phospholipids. Cholesterol has specific functions in the membrane. For example, it gives rigidity or stability to the cell membrane and prevents crystallization of hydrocarbons.
The biomembranes also contain sugar molecules called glycolipids. These are lipid molecules that microaggregate in the membrane. Certain kinds of molecules are bounded by sphingolipids as cholera and tetanus toxins. Sphingolipids and cholesterol favour the aggregation of proteins in microdomains called rafts. As functions, the glycolipids are protective and insulators and play the role of platforms for the attachment of proteins as the membranes are moved around the cell and also during signal transduction (Simons and Ikonen, 1997; Brown, 1998).
The proteins constitute another component of the cell membranes. They present as giant macromolecules. There are essentially two kinds of proteins, namely integral or transmembrane and peripheral proteins. The former are amphipathic and formed by hydrophobic and hydrophilic regions having the same orientation as the other lipid molecules (Tamm, 2005). Their function is to transport substances across the membrane like ions and macromolecules, energy and information coming from the outside. The peripheral proteins are linked to the cytoplasm surface by fatty acyls chains. Particularly, they protect the membrane surface, regulate cell signalling and participate in many other important cellular events (McLaughlin et al., 2002). The proteins possess have a rich architecture we do not precise here. For more details concerning architecture proteins, structure, composition and function of the cell membranes, the reader could consult the textbooks by Finkelstein and Ptitsyn (2002) and by Yawat (2003), respectively.
The positions of lipid molecules on the membrane surface are not fixed in space. Indeed, these effectuate free movements termed lateral diffusion (Almeida et al., 1992). But, under certain circumstances, these lipid molecules can also jump from one side to the other. This is the flip-fop diffusion. Moreover, a lipid molecule may rotate around its principal axis (rotational diffusion). Lateral and rotational diffusions confer to the membrane its liquid characteristics, but with the constraint that the hydrophobic chains keep their parallelism and remain perpendicular to the surface of the bilayer. In fact, this order is similar to that usually encountered in the liquid-crystals context (De Gennes and Prost, 1993). To sum up, we can say that, from thermodynamics point of view, the stability of the biomembrane is largely determined by the nature of motion of its lipid molecules.
Like usual thermodynamic systems, bilayer membranes may undergo phase transitions (Stanley, 1971; Itzykson and Drouffe, 1989; Zinn-Justin, 1989) by a simple variation of a suitable parameter. The latter may be temperature, lateral pressure, or ionic forces. These phase transitions are either first or second order. In this study, we shall restrict ourselves to second order phase transition, only. This means that, we are interested in those biomembranes that exhibit a critical point. The common characteristic of these systems is that, in the critical region, they can be described by few parameters and the dependence on these parameters presents a universal character. In addition, at the critical point, the system becomes scale-invariant. In other word, the corresponding correlation length diverges as the transition temperature is approached. We recall that, each critical system belongs to a special universality class that is generally characterized by two numbers, namely the number of components of the order parameter, n and the space dimensionality, d. The critical biomembranes we consider belong to the (n = 1, d) universality class, as Ising-like magnetic materials (Stanley, 1971; Itzykson and Drouffe, 1989; Zinn-Justin, 1989).
To present a large scope for studying critical phenomena within bilayer biomembranes, we shall be concerned with four interesting physical situations, which are (1) lateral and transversal phase separations between unlike phospholipids, (2) phase separation between phospholids and cholesterol molecules, (3) lateral phase separation between phospholipids and grafted polymer chains onto biomembranes and finally (4) membrane adhesion.
LPS AND TPS BETWEEN PHOSPHOLIDS
In most cases, the lipid molecules inside the bilayer are of different chemical structure. This means that they experience (relatively small) mutual segregation forces. As a consequence, under some conditions explained below, one assists to the appearance of domains formed by chemically incompatible species. This separation process has been observed within natural systems, such as cells and vesicles. Notice that the mechanism of the formation of domains is similar to that governing the traditional phase separation that takes place varying temperature, for instance. The integration of a strange molecule in the bilayer may also lead to a rearrangement of lipid molecules into domains alternatively rich in unlike components. Essentially, there exist two kinds of chemical incompatibilities. The lipid molecules can aggregate on each leaflet and form domains. This is the Lateral Phase Separation (LPS). The latter may also occur in the presence of ions (Ca+2, for instance) (Almeida et al., 1992), around an incorporated macromolecule, or by a change of temperature (Binder et al., 2003). The other possibility is that, the two leaflets of the bilayer may have different compositions and then, the lipid molecules undergo a transversal phase separation (TPS), where one species jumps from a leaflet towards the preferred one. The TPS may also produce by an adsorption of a convenient polymer (Binder et al., 2003). In the two cases, the separation mechanism is controlled by different interactions, namely the forces between hydrophilic polar-heads and between hydrophobic tails. In fact, a variation of the external pH yields a change of the electric charge of the polar-head. As a consequence, the attractive forces between two adjacent polar-heads are reduced. The introduction of some ions can also lead to a redistribution of lipid molecules, due to the formation of complexes between polar-heads and metallic ions. The adsorption of ionic polymers onto the two leaflets may increase the density of lipid molecules, which experience attractive mutual electrostatic interactions. A phase separation can also occur varying the temperature of the bilayer composed of two lipid molecules of different melting temperatures. To understand the organization of lipid molecules on the two leaflets, we first focus on a special phase separation that may produce under small variations of the bilayer structure. A typical example is provided by phosphatidylcholine mixtures (Knoll et al., 1991; Silvins et al., 1996), when the acyls chains are of different lengths but of the same chemical nature. Their polar-heads are identical but the length difference induces segregation forces between unlike chains. Second, the attention is paid to the influence of cholesterol and grafted polymers on the organization of lipid molecules within biomembranes.
To comprehend the thermodynamic mechanism of the phase separations within lipid membranes, we consider, as example, a bilayer composed of two kinds of acyls chains of different lengths. We shall denote by T, Φ1 and Φ2, Δ1, κ and Δc0, the absolute temperature, the compositions of one component on the two leaflets, the length difference, the bending rigidity constant of the membrane and the curvature asymmetry gap, respectively. If the mixture is assumed to be incompressible, then, the compositions of the second component on the two sides of the bilayer are simply 1-Φ1 and 1-Φ2. Therefore, the phase separation between unlike lipid molecules is controlled by four kinds of relevant parameters (T, Δ1, κ, Δc0). We note that the dependence on temperature can be taken into account through the contact Flory interaction energies (per kBT unit) χ11, χ22 and χ12 (Benhamou et al., 2008). The former describes the effective interaction energy on leaflet 1, the second on leaflet 2 and the third between leaflets 1 and 2. For both LPS and TPS, χij>0. These conditions traduce the segregation phenomenon on each side of the bilayer.
Now, to investigate the phase diagram, we introduce two order parameters, φ and ψ, which are nothing else but the composition fluctuations of one species on the two sides.
Also, these fields are the composition differences of the considered components on the two leaflets. It has been shown (Benhamou et al., 2008) that the free energy governing physics is:
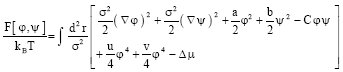 | (1) |
Here, T accounts for the absolute temperature, kB for the Boltzmann’s constant, σ for the polar-head size, u and v for the (positive) coupling constants and C describes the coupling between the two leaflets. There, Δμ is the chemical potential difference of the two species. It was found (Benhamou et al., 2008) that the coefficients a, b and C can be related to the length difference Δ1 and curvature gap Δc0 by:
| (1a) |
| (1b) |
| (1c) |
The last equality clearly shows that there is a competition between the length difference of acyls chains and curvature gap. When the former dominates, C>0 and a LPS is then expected. In the opposite case, we have the condition that C<0 and the system undergoes rather a TPS. It was demonstrated (Benhamou et al., 2008) that the critical temperature, Tc, is given by:
| (2) |
where the positive sign is for LPS and negative one for TPS. The above equation defines a critical line in the (T, C)-plane along which the bilayer exhibits a separation transition.
With the help of free energy (1), we extract the phase diagram shape. This can be done minimizing this free energy with respect to the (uniform) order parameter φ and ψ, that is: δF/δφ = 0 and δF/δψ = 0. This gives:
| (3) |
| (4) |
At equilibrium, that is for, it was found (Benhamou et al., 2008) that the total order parameter, Φ = φ+ψ, behaves near the critical point, as:
| (5) |
| (6) |
with the critical exponent β0 = 1/3. Here, Φ0 is some known amplitude.
At the critical temperature, the total order parameter scales as (Benhamou et al., 2008)
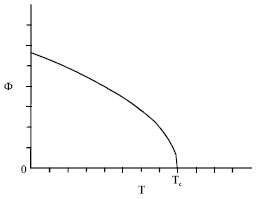 | |
| Fig. 1: | Overall order parameter versus temperature at Δμ = 0 |
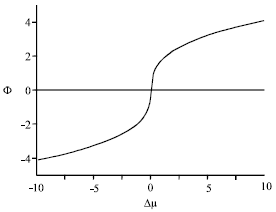 | |
| Fig. 2: | Overall order parameter versus chemical potential difference, at the critical temperature |
| (7) |
with the critical exponent γ0 and the known new amplitude Φ1.
In Fig. 1 and 2, we report the overall order parameter Φ upon temperature (at Δμ = 0) and upon chemical potential difference (at the critical point), respectively.
On the other hand, it has been shown (Benhamou et al., 2008) that the total thermal compressibility, κtot = δΦ/δΔμ|Δμ = 0, behaves as:
| (8) |
with a new critical exponent γ0. Notice that the associated amplitude is not the same above and below the critical temperature.
Other quantities of interest are the partial structure factors Sφn (q), Sψψ (q), Sφψ (q) and SΨφ (q), which inform on the critical phase behaviour. These are noting else but the Fourier transforms of the correlation functions constructed with two fields φ, two fields ψ and one field φ and one field ψ, respectively. According to Ouarch et al. (2009), these structure factors have the following exact expressions:
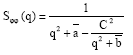 | (9a) |
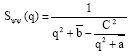 | (9b) |
| (9c) |
with the notations
| (9d) |
where φb and ψb are the equilibrium order parameters that are solutions to the coupled equations (3) and (4), with Δμ = 0. There, q is the modulus of the wave-vector. The value of these structure factors in the zero-scattering angle limit (q→0) gives the partial thermal compressibilities.
LPS BETWEEN PHOSPHOLIDS AND CHOLESTEROL
The biomembranes may also undergo another type of phase separation. This latter produces between phospholipids and cholesterol and one assists to the appearance of rafts (Simons and Ikonen, 1997; Anderson and Jacobson, 2002), which are liquid domains rich in cholesterol. Also, these rafts may be domains composed of saturated lipids (sphingomyelin lipids), or particular proteins (Brown and London, 2000). This phase separation was observed using fluorescence microscopy (Silvins et al., 1996; Korlach et al., 1999; Dietrich et al., 2001; Feigenson and Buboltz, 2001; Veatch and Keller, 2002; Baumagart et al., 2003; Gaus et al., 2003) and NMR and calorimetry (Vist and Davis, 1990; Sankaram and Thompson, 1990). We note that this special phase separation has recently shown to have some relevance to signals transduction and membrane traffic (Sankaram and Thompson, 1990).
From a theoretical point of view, the lipid-cholesterol phase separation were extensively studied (Komura et al., 2004; Allender and Schick, 2006). The first theory (Komura et al., 2004) was based on a one-order parameter model, which takes into account the couplings between the local composition and the internal membrane structure. For this theory, the order parameter is the relative bilayer thickness and the goal was a quantitative investigation of the first-order phase separation in binary mixtures of saturated/unsaturated lipids and lipid/cholesterol. Few years after, another theory (Allender and Schick, 2006) was introduced. The latter was constructed introducing two order parameters and taking into account the coupling between the sides of the membrane. These order parameters are the distance of the cholesterol composition from its critical value and the relative increase of the thickness of the outer leaflet at the critical point (Komura et al., 2004, 2005). Using this second theory, the authors drawn all phase diagrams related to the lipid-cholesterol LPS.
Despite their simplicity, the predictions from the elaborated models (Allender and Schick, 2006; Komura et al., 2005) were found to be in agreement with experimental data. But the very recent theory introduced by Benhamou et al. (2008) seems to be more consistent and coherent and it can be regarded as a general scope for studying the phase separations within biomembranes.
LPS BETWEEN PHOSPHOLIPIDS AND GRAFTED POLYMER CHAINS
We first note that the majority of macromolecules forming the bilayer are simply anchored on the membrane surface and form a soft branched polymer brush (Aubouy, 1998). Most of studies dealt with grafted polymers onto bilayer membranes were motivated by their potential applications in biological materials, such as liposomes (Ringsdorf and Schmidt, 1986; Lasic, 1992; Torchilin, 1996; Joannic et al., 1997). These artificial vesicles may be synthesized from natural untoxic phospholipids and cholesterol, or from diblock-copolymer solutions.
Consider a membrane with grafted linear polymer chains by one extremity (Fig. 3). The latter is a big lipid molecule called anchor. It is assumed that the phospholipids and anchors are chemically incompatible. This means that one is in the presence of a chemical segregation. It is also supposed that the grafted polymer chains effectuate free movement on the membrane surface. By a change of a convenient parameter like temperature, pressure or membrane environment, a phase separation may produce between the host lipid molecules and anchors. Such a LPS has been first studied by Aubouy (1998), by considering, for simplicity, that the substrate is a planar surface. The problem was re-examined in a very recent work (Benhamou et al., 2007). The main difference is that, in the new work, the influence of the membrane undulations on the LPS is taken into account.
To investigate the associated phase diagram, one needs the mixing free energy expression, F[Φ]. The latter was derived in Benhamou et al. (2007) and it was found that its dependence on the anchor volume fraction, Φ, writes:
| (10) |
Here, q denotes the ratio of anchor area to that of polar-heads of phospholipids (that must not be confused with the wave-vector modulus), A is constant coefficient of the order of unity, N accounts for the common polymerization degree of grafted polymer chains. There, the segregation parameter χ is the sum:
| (11) |
 | |
| Fig. 3: | A biomembrane with anchored polymer chains, each by one big amphiphile molecule |
The two parts are positive definite. The first represents the usual segregation parameter traducing the chemical mismatch between the host phospholipids and anchors. The last comes from the membrane undulations. This extra contribution is nothing else but the spatial integral of the attractive induced pair-potential between anchors we do not write (Benhamou et al., 2007; Marchenko and Misbah, 2002). The essential result is that, the parameter χm scales as (Benhamou et al., 2007).
| (12) |
where κ is the bending modulus. For example, if κ = 25 kB, χm is of the order of 0.2 (per kBT unit). The above behaviour indicates that the effective attraction phenomenon between species of the same chemical nature is relevant only for those biomembranes of small bending rigidity constant.
Recall that the temperature dependence of the segregation parameter is as follows (Benhamou et al., 2007):
| (13) |
Coefficients α and β depend on the chemical structure of unlike species and membrane characteristics (through the bending modulus).
We restrict ourselves to the spinodal curve, along which the thermal compressibility diverges. It is obtained writing δ2 F/δΦ2, where F is the above mixing free energy. Without details, we report in Fig. 4 the variation of the critical segregation parameter upon composition Φ.
In this approach, we assumed that the grafted chains are monodisperse. Actually, these chains are rather polydisperse, that is their lengths are distributed at random. As shown by Benhamou et al. (2007), the polydispersity increases the segregation parameter. This can be understood as follows. In the presence of grafted polymer chains with different lengths, the excluded volume interactions are reduced in comparison to the monodisperse system. We recall that the LPS is the consequence of a competition between the excluded volume forces between monomers belonging to grafted chains, the chemical segregation between phospholipids and anchors and the membrane undulations.
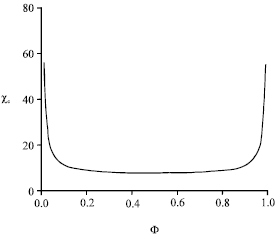 | |
| Fig. 4: | Critical segregation parameter versus anchor volume fraction (spinodal curve) |
MEMBRANE ADHESION
We start from a lamellar phase composed of two parallel (neutral) fluid membranes. The cohesion between these bilayer membranes is ensured by long-ranged attractive van der Waals forces (Israelachvili, 1991). These are balanced, at short membrane separation, by strong repulsion coming from hydration forces (Rand and Parsegian, 1989) and by steric shape-fluctuations ones resulting from the membrane undulations (Helfrich, 1973).
For two parallel bilayer membranes separated by a finite distance, H, the total interaction energy per unit area is:
| (14) |
The first contribution
| (14a) |
represents the hydration potential (per unit area) that acts at small separations of the order of 1 nm. The amplitude Ah and potential-range λh are about Ah = 0.2 J m-2 and λh. The second contribution
| (14b) |
accounts for the attractive van der Waals potential (per unit area). The latter originates from polarizabilities of lipid and water molecules. The Hamaker constant W is in the range W = 10-22-10-21 J and δ∼4 nm for the bilayer thickness. The last contribution is the steric shape-fluctuations potential (per unit area) (Helfrich, 1973).
| (14c) |
where, kB is the Boltzmann's constant, T the absolute temperature and κ the common bending modulus of the two membranes. If the two adjacent bilayers have different bending rigidity constants κ1 and κ2, we have κ =κ1 κ2/(κ1+κ2). There, the coefficient ch is a known numerical coefficient (Helfrich, 1973).
Notice that the lamellar phase remains stable at the minimum of the potential, provided that the potential-depth is comparable to the thermal energy kBT. In particular, this depth depends on the value of amplitude W of the direct van der Waals energy. In fact, the Hamaker constant W may be varied changing the polarizability of the aqueous medium.
In a seminal study, Lipowsky and Leibler (1986) have demonstrated that there exists a certain threshold Wc beyond which the van der Waals attractive interactions are sufficient to bind the membranes together, while below this characteristic amplitude, the membrane undulations dominate the attractive forces and then, the membranes separate completely. According to the authors, Wc is in the interval Wc = (6.3-0.61)x10-21J, when the bending rigidity constant is in the range κ = (1-20)x10-19J. We note that the typical value Wc corresponds to some temperature, Tc, called unbinding critical temperature (Lipowsky and Leibler, 1986; Lipowsky and Sackmann, 1995). In particular, it was found (Lipowsky and Leibler, 1986) that, when the critical amplitude is approached from above, the mean-separation between the two membranes, ⟨H⟩, diverges according to:
| (15) |
with the critical exponent
| (15a) |
The latter was computed using field-theoretical Renormalization-Group (Lipowsky and Leibler, 1986).
Now, for charged membranes forming the lamellar phase, it was demonstrated (Lipowsky and Leibler, 1986) that the mean-separation between two adjacent bilayers scales as:
| (16) |
where n is the ionic concentration of the aqueous medium (that must not be confused with the number of components of the order parameter evoked above) and nc is its critical value. Of course, the latter depends on the nature of the lipid system. For instance, for DPPC in CaCl2 solutions, experimental measurements (Lis et al., 1981) showed that nc is in the range 10-84 mM.
We note that, for T>, the shape-fluctuations drive the membranes forming lamellar phase apart even in the presence of the direct attractive forces. In this case, the system recovers its bound state by a simple application of an external pressure or a lateral tension.
In the presence of an external pressure P, it was found (Lipowsky and Sackmann, 1995) that the mean-separation ⟨H⟩ scales as:
| (17) |
This behavior agrees with MC data (Lipowsky and Zielinska, 1989).
The role of a lateral tension is to suppress the bending undulations and the fluctuation-induced repulsion. In fact, the latter becomes short-ranged and the long-ranged van der Waals attraction then dominates (Lipowsky and Leibler, 1986). For this case, it was found (Lipowsky and Sackmann, 1995) that the mean-separation behaves as:
| (18) |
where, Σ represents the lateral tension.
In this study, we reviewed the essential of thermodynamic study of phase transitions within bilayer biomembranes. More precisely, we were interested in phase separations between unlike molecules forming the bilayer and membrane adhesion. These studies were achieved from a static point of view. This means that critical dynamics has not been discussed. We recall that critical dynamics of LPS and TPS was studied in details in a recent work (Ouarch et al., 2009).
As we pointed out above, the phase separations may be caused by a change of a suitable parameter, such as temperature, lateral pressure of ionic forces. Two phase separations are possible, namely lateral or transversal transitions. The nature of separation crucially depends on the mutual interactions between unlike molecules within the bilayer and on other factors (length and non-saturation degree of acyls chains, curvature asymmetry, etc.). The majority of situations require the introduction of two-order parameter models, since the composition is not generally the same on the two leaflets of the membrane. This can be easily seen noting that the areas of interior and exterior membrane surfaces are not identical. In addition, the ionic environment is not the same near the two sides.
The first step was the investigation of LPS and TPS between unlike phospholipids. As we have shown, the associated phase behavior is essentially controlled by the structure of amphiphile molecules (through the length of their hydrocarbon chains) or by curvature asymmetry, at fixed temperature. When the structure dominate, a LPS is then favoured. For the opposite situation, the strong curvature asymmetry imposes to the phospholipid mixture to transversally phase separate.
Thereafter, we were interested in another LPS that produces between phospholipids and cholesterol within biological membranes. Such a phase separation is accompanied by the appearance of rafts that are small liquid domains rich in cholesterol. These rafts protect the proteins assembly on the membrane surface. This transition is largely studied from a theoretical and experimental point of view (Komura et al., 2004, 2005; Allender and Schick, 2006).
We have extended discussion to LPS between phospholipids and grafted polymer chains onto a bilayer biomembrane. It is known in literature that the macromolecules anchored to the membrane phase separate by a variation of few 30% of the surface pressure and form domains (Keller et al., 1998). Also, in very recent experiments (Salditt et al., 1997), a LPS was also observed in lamellar phases of DNA-lipid complexes. The authors reported on X-ray diffraction the structural studies of linear DNA chains that are adsorbed on cationic membranes in the lamellar phase of cationic lipid-DNA complexes. We recall that these biological materials are recently used in nonviral gene therapy clinical applications (Warriner et al., 1998; Martin-Herranz et al., 2004).
We have not discussed another LPS from bilayers formed by a surfactant and its co-surfactant, which is caused by a strong curvature asymmetry, where one species (surfactant or its co-surfactant) prefers to be located on the leaflet of positive curvature. As noted by Benhamou et al. (2008), such a system can also be modelled using a two-order parameter theory.
At the end, we discussed a special phase transition that occurs between two adjacent bilayers we termed membrane adhesion or unbinding transition. The latter takes place at some typical value of the van der Waals potential amplitude. Generally, the adhesion occurs by a change of medium polarizability or temperature. Some important details, such as the presence of inclusions, were not taken into account. But this can be done noting that these inclusions have as effects to additively renormalize the elastic constants of the bilayer.
Finally, the quality of solvent (selective, good or theta solvent) that surrounds the lipid membrane and other complexities may also affect these phase transitions. Such problems are under consideration.