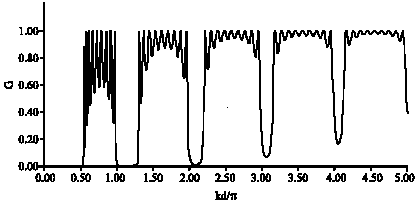
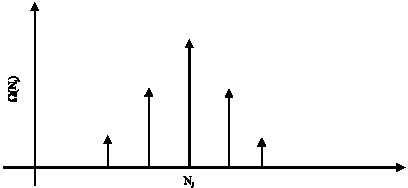
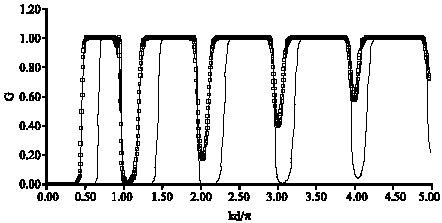
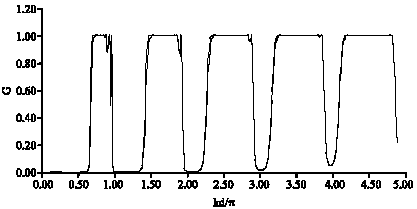
Research Article
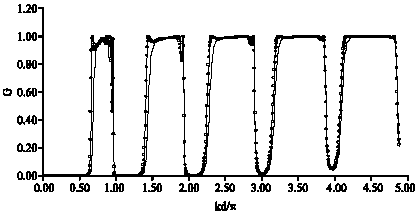
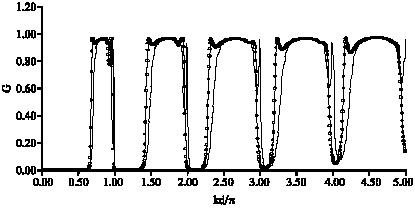
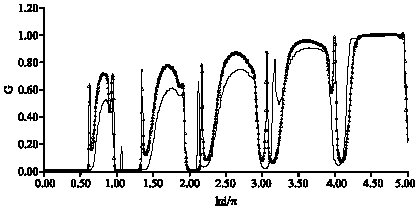
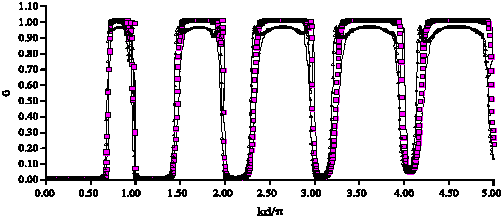
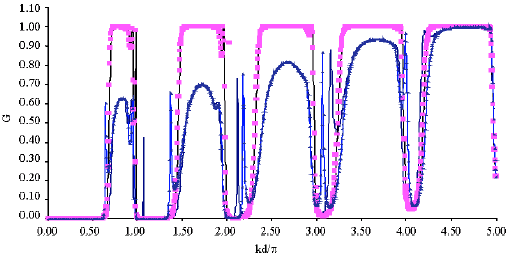
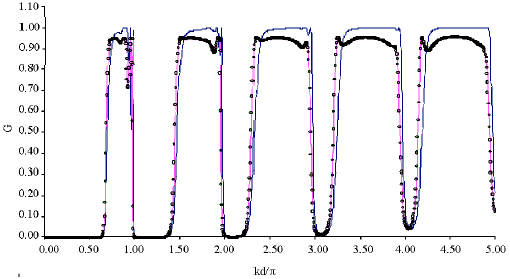
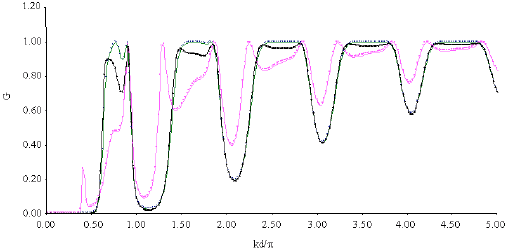
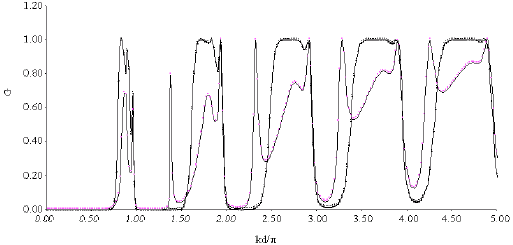
Study of Defects Effect on Electronic Conductance Through Binomially Tailored Quantum Wire
Department of Physics, Al-Azhar University of Gaza, Gaza Strip, Palestinian Authority
A.I. Assad
Department of Physics, Al-Aqsa University, Gaza Strip, Palestinian Authority