ABSTRACT
The fluctuations of laser light by inhomogeneous surfaces have been investigated in the light of two scattering models: The discrete random walk-and the phase screen-models. By assuming a complex Gaussian field distribution, the filed autocorrelation functions are found to be space and time dependent and that the inhomogeneous infinite nature of most distant bodies can be studied using these models.
PDF Abstract XML References Citation
How to cite this article
URL: https://scialert.net/abstract/?doi=rjp.2007.60.63
INTRODUCTION
The uniqueness of the laser light seems strange when looked at from classical viewpoint as it depicts characteristics that are obviously striking (it deviates only from strict parallelism due to diffraction from the exit of the aperture; coherency; monochromatic; high contrast ratio etc). No wonder the early scientist referred to it as a problem looking for solution (Jeff, 1994).
Generally, the effects observed in the fluctuation of scattered light have geometrical origin being a result of refraction by large-scale random variations in refractive index. These fluctuations are caused mainly by density variations within the propagating medium, such as the atmosphere, or by roughness of the boundary between media having different dielectric constants. In astronomical concept, significant dispersion may also be observed for instance, in the case of the colourful twinkling of a star low down in the sky, which for the most part are white light optical effects that are independent of the wavelength within the visible spectrum. With the advent of the laser, a new range of coherent light scattering phenomena became visible to the naked eye. In particular, the random interference effect that has come to be known as Laser speckle commonly occurs in laboratory laser light scattering experiments (Dainty, 1975). In actual fact, laser light scattering generates many diffraction, interference and geometrical optical effects that can be detected within the optical wavelength, which has embedded in it, the nature of the scattering surface. This same effect is now achievable at other frequencies of the electromagnetic spectrum. For instance, the observed desertion of the short wave radio reception due to ionospheric fluctuations. Based on these light fluctuations, many theoretical results have been derived at these longer wavelengths. For example, an early theoretical description of random interference effects was developed to explain the fluctuating radar return from raindrops twenty years before the visual appearance of the equivalent laser generated phenomenon known as speckle.
The aim of the present research is to investigate and develop a model for the investigation of the information revealed by dispersive surfaces (which is the real nature of most objects) like celestial bodies and any other objects (both far and near) on scattering laser light. The result is envisaged to be of uttermost importance in the general study of the nature of distant objects and will help in general design of equipments needed for investigating these phenomena.
THEORETICAL FRAMEWORK
Optical instability (fluctuation) phenomenon is one of the most familiar optical phenomena for many reasons: They are fundamental information source depicting the nature of the scattering medium that enables and enhances the understanding of the overall nature and motion of the individual scattering centres such as their dimension and temporal evolution. Also, they serve as clutter source that modulates the signal carrying information of interest (Bernes, 1976).
Many theoretical models (each with its boundary conditions) have been proposed to explain some of these observed phenomena. These models are not only vital in practical implementation but also an asset in dealing with the range and scale of the scattering medium. Two most conventional models are the discrete random walk model and the phase screen model for studying the scattering caused by continuous inhomogeneous media and rough surfaces (Sheng, 1985). Knowing too well that real surfaces are mainly dielectric in nature, we will adopt these two models to investigate starting from the preliminary assumption of homogeneous media and later introduce the polarization factor due to the nature of scattering surfaces to investigate how laser light are modulated by such surfaces.
SCATTERING MODELS
Here we analyze the two basic scattering models with their appropriate boundary condition(s).
Discrete Random Walk
Basically, the Discrete Random Walk (DRW) model is applied to decomposable large systems made up of independent scattering centres. To investigate the relationship between the intensity and field autocorrelation functions, we measure simultaneously the fluctuations in the scattered field and amplitude, which is normally linked by the Siegert relation. Since the scattering intensity, ![]() , the intensity correlation function, G2 (τ) for (N>>1) is:
, the intensity correlation function, G2 (τ) for (N>>1) is:
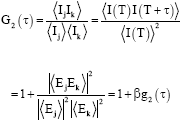 | (1) |
where, N is the number of scattering surfaces and β is the coherent factor very close to unity and normally determined by the geometry of the detector and the subscripts j, k denotes initial and final configurations of the electric filed vector. As given by the Siegert relation, in the complex random Gaussian fields, the correlation function g2 (τ) relates with the field correlation function as:
| (2) |
Hence, (1) can rewritten as
| (3) |
where, g1 (τ) is the autocorrelation of the scattered field given as
| (4a) |
and for a normalized field, we have that
| (4b) |
where, T is the time scale of which the measurement of the fluctuations distinct from the propagation time t of the field in the medium (t<<T)).
Equation 4 tells us that a complex Gaussian random variable can be used to represent scattered wave field and the Siegert relation only holds for multiply scattered wave field. However, if the induced polarization of the media is considered (Cummins and Pike, 1973), which is the case for real surfaces, Eq. 1 becomes:
| (5) |
| Where, | 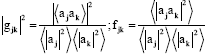 |
Phase Screen Model
The phase screen model is more or less like the well-known tangent plane wave approximation for an infinite scattering medium, which assumes that an incident optical field (laser light) Eo subjected to multiple phase distortion that induces a scattering field ![]() of the form:
of the form:
| (6) |
Using Huygens’s principle in the limit that the phase fluctuation is far greater than the wavelength, λ the nature of the field propagation is evaluated as:
| (7) |
where, ![]() is transverse to the direction of propagation, z (Beckman and Spizzichino, 1963).
is transverse to the direction of propagation, z (Beckman and Spizzichino, 1963).
Equation 7 is a model equation encompassing wide range of phenomena with Ψ acting as the statistical determinant of the model equation. The calculation of the phase fluctuation induced by the random phase screen (for instance celestial bodies) is only achieved to high degree of accuracy using computer simulations (Schultz-Dubois, 1983). However, assuming a complex Gaussian signal, the phase derivative distribution (joint probability distribution) (P (ΨT,Ψ*T)) at times t and t΄ = t+τ is a student t distribution with infinite variance and this gives the statistics of the phase difference:
| (8) |
with a nonlinear correlation function usually of the field ![]() and is the covariance matrix. Assuming a normalized field according to Goodman (1985), ⟨Ψi* Ψj⟩ = ⟨|Ψ(t)|2⟩ = 1and ⟨Ψi* Ψj⟩ =g1 (τ) we obtain the autocorrelation function of the field in terms of amplitude and phase
and is the covariance matrix. Assuming a normalized field according to Goodman (1985), ⟨Ψi* Ψj⟩ = ⟨|Ψ(t)|2⟩ = 1and ⟨Ψi* Ψj⟩ =g1 (τ) we obtain the autocorrelation function of the field in terms of amplitude and phase ![]() as:
as:
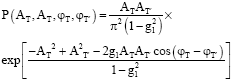 | (9) |
Since most surfaces (real surfaces) are infinite inhomogeneous and rough surface (pressure gradient varies both with time and altitude) causing a thin turbulent layer in the intervening medium, the phase screen model can be applied to determine the evolution of the electric field component in such media.
CONCLUSIONS
It has been shown that the understanding of the whole phenomenon surrounding the scattering of laser light by infinite (even finite) inhomogeneous systems which depicts real surfaces can in general be of uttermost importance in determining the nature of these scattering surfaces especially those that we do not have direct perception about their spatiotemporal nature. This has been investigated in the light of two models: the discrete random walk model and the phase screen model. In both cases, it was observed that the fields depict Gaussian fields. For the discrete random walk model, the intensity and field autocorrelation functions induced by the scattering surface is linked by the Siegart relation (Eq. 1-5) while the phase screen model can be applied taking cognizance of the joint probability distribution ![]() which has embedded in it the phase fluctuations induced by the scattering surfaces (Eq. 7-9).
which has embedded in it the phase fluctuations induced by the scattering surfaces (Eq. 7-9).
ACKNOWLEDGMENTS
The Almighty God has always been my strength. All that I am is His. Also to my entire family and friends for their moral supports.








