ABSTRACT
This research used the Linear elastic fracture mechanics relation together with that of the stress intensity factor range after substituting the material constants A, M developed from the outcome of an experiment conducted on a high yield strength (σy = 100 Ksi (689 MN/m2), critical stress intensity factor (Kc) = 150 Ksi [in]1/2 (165 MN/mm2)) Martensitic steel in air environment to develop a working model which was then employed with different constant amplitude stresses and varying average crack lengths to generate data. Series of regression analysis and optimization processes were employed to create a novel model which is suitable for data analysis, generation of design consideration, evaluation and determination of damage tolerance and safe operating condition. This has been used to eliminate the many mathematical steps and processes involved in data analysis and add ease to design and evaluation.
PDF Abstract XML References Citation
How to cite this article
URL: https://scialert.net/abstract/?doi=rjp.2007.55.59
INTRODUCTION
Crack, a phenomenon which have been described as the alternative opening and closing of regions, beginning from a notch hole (Odukwe et al., 2007), initiates unnoticed and grow at a fast rate through structural members and have been found to be the cause of most fatigue failures (Sobcyzyk, 1987; Miller and Akid, 1996; Budynas, 1998; Shaffer et al., 1999; Henkel and Pense, 2001). These failures are sudden and occur at points of stress raisers and can lead to catastrophic effects if allowed to develop further than the material can withstand (Tomkins et al., 1981; Miller and Akid, 1996; Courtney, 2000; Dieter, 2000). The extent to which crack grows in a material depends on its brittleness (Dieter, 1988; Shaffer et al., 1999). However, brittle fracture is characterized by a rapid rate of crack propagation, having no gross deformation, but containing little micro deformation in deference to the other type known as ductile fracture, which is characterized by appreciable amount of plastic deformation prior to and during crack propagation, with an amount of gross deformation present at the crack surface (Dieter, 1988; Shaffer et al., 1999).
Many attempts have been made at studying the phenomenon of crack initiation and growth with the aim of creating suitable mathematical models which can be used to study and also understand the behaviour of structural members under variable loading and different environments (Nelson, 1984; Sobcyzk, 1987; Nelson, 1990; Navarro and De Los Rios, 1992; Hirose, 1993; Miller and Akid, 1996; Pascual and Meeker, 1997; 1999). The first by Griffith for fracture behaviour of components that contains sharp discontinuities and its modification by Irwin and Orowan are available (Anderson, 1995). It was assumed that incipient fracture in ideally brittle materials occur when the magnitude of the energy supplied at the crack tip during incremental increase in crack length is at least equal to the magnitude of the elastic energy. The result was that crack growth will take place when the elastic energy per unit crack surface area is equal to the material resistance to crack extension (Ajayi, 2003). Thus, once a flaw is initiated in a material, it can grow when certain conditions are met. This growth thence can result in eventual failure if the conditions reach a critical value. Moreover, it has been certified that changes in stress intensity factor, Δk, has a major influence on the fatigue crack growth (Odukwe et al., 2007), thereby justifying the model known as the Paris equation (Sobcyzk, 1987; Ewalds and Wanhill, 1991; Navarro and De Los Rios, 1992; De Los Rios et al., 1994; Miller and Akid, 1996), which relates the differential of the fatigue crack growth per cycle of loading to the stress intensity factor range (Δk) given as:
| (1) |
Where A, M are material constants and ![]() is the rate of crack growth per cycle of loading.
is the rate of crack growth per cycle of loading.
The Eq. 1 above has been used to explain the phenomenon of linear elastic fracture mechanics, given as region II in a log-log plot of ![]() against Δk (Dieter, 1988; 2000). Further work on this equation for high yield strength (σy = 100 Ksi (689 MN/m2), critical stress intensity factor (Kc) = 150 Ksi [in]1/2 (165 MN mm-2). Martensitic steel in air environment by Odukwe et al. (2007), reveal thatΔk explains about 99.85% 0f changes in
against Δk (Dieter, 1988; 2000). Further work on this equation for high yield strength (σy = 100 Ksi (689 MN/m2), critical stress intensity factor (Kc) = 150 Ksi [in]1/2 (165 MN mm-2). Martensitic steel in air environment by Odukwe et al. (2007), reveal thatΔk explains about 99.85% 0f changes in ![]() and also gives the material constants A and M as 7.244x10-9 and 2.22, respectively. A model representing a straight line approximation of Eq. 1 was then proposed as:
and also gives the material constants A and M as 7.244x10-9 and 2.22, respectively. A model representing a straight line approximation of Eq. 1 was then proposed as:
| (2) |
Thus, the Equation becomes useful for the metal when right substitutions are made into it. However, the process becomes cumbersome when it is desired to have design consideration to study the behaviour of metals to changes in the constant stress amplitude and varying fatigue cycle of loading, thereby making it imperative for researchers to look into various ways of creating simple models which will eliminate too many compulsory substitution, reduce mathematical steps and also will be suitable for data analysis. This work aims at achieving this by carrying out applied research using Eq. 1, stress intensity factor relation together with the parameters developed in Odukwe et al. (2007) to create a novel model which will be devoid of many mathematical processes, but suitable for analyzing the crack sizes from the point of view of number of fatigue cycles and constant amplitude stresses.
MATERIALS AND METHODS
The Eq. 1 together with the relation for the stress intensity factor range given by Eq. 3 and the parameters developed in Odukwe et al. (2007) were employed to develop a simple working model which can be used to generate data. Constant amplitude stresses of 15 Ksi (103.43 MPa) to 60 Ksi (413.70 MPa) in increment of 5ksi (34.48 MPa) were used along side average crack lengths ranging from 0.20 inches (5.08 mm) to 3.95 inches (100.33 mm).
| (3) |
Where C = constant for edge and surface cracks = 1.12 (Odukwe et al., 2007), σ and a are the constant amplitude stress and the average crack length, respectively.
Substituting Eq. 3 into Eq. 1 and simplifying gives:
| (4) |
Integrating from No to Nf gives:
| (5) |
Substituting the values of A, M and C given earlier into Eq. 5 gives:
| (6) |
Thus, inputting the various values of average crack lengths for desired constant amplitude stress of 15 ksi (103.43 MPa) into Eq. 6 gives Table 1.
Carrying out a regression analysis of a on the vertical against N on the horizontal for constant amplitude stress of 15 ksi (103.43 MPa) gives an exponential relationship after optimization as:
| (7) |
To get a general relationship for all values of amplitude stress, different values of σ were used and the result of the regression of a against N for different data points are as presented in Table 2.
RESULTS AND DISCUSSION
Table 1 and 2 shows that a pre-existing crack size of 0.20 inches (5.08 mm) was used and that the exponential variable changes with changing σ, while the R2 values gives a justification that the number of cycles explains about 99.8% changes in the crack sizes. The 0.18 value is related to the initial crack length. Thus, the general form of the estimated relationship can be given as:
| (8) |
where a = final crack length,
ao = initial crack length, α = exponential variable and N = Number of fatigue cycles.
Observing column one with column three shows the relationship that:
| (9) |
Regressing column one against three and optimizing the result gives the power law denoted by:
| (10) |
With this result, it is clear that σ is responsible for the observed changes in the exponential variable, hence, substituting Eq. 10 into Eq. 8 gives:
| Table 1: | Table showing the number of cycles of loading corresponding to desired crack sizes, obtained from substituting the values of individual average crack size and desired constant amplitude stress of 15 Ksi into Eq. 6 |
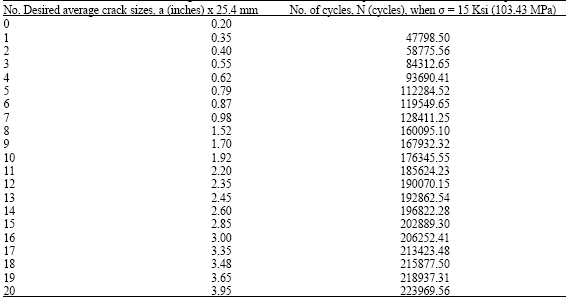 | |
| Table 2: | The result of regression analysis of average crack sizes a, against Number of cycles, N for different values of constant amplitude stresses, σ |
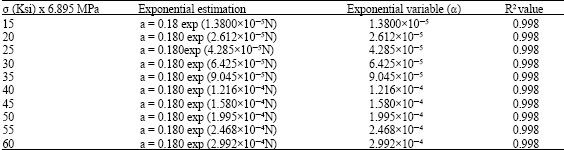 | |
| (11) |
and the general equation thus can be written as:
| (12) |
This Eq. 12 therefore, is a constitutive relationship connecting crack size a, with the number of cycles, N and stress amplitude, σ for Martensitic steel containing edge and surface cracks. Thus with this model, corresponding crack lengths can be deduced from knowledge of desired number of fatigue cycles and constant amplitude stress. No reference is made whatsoever to the constants A, M and C which are compulsory parameters for the use of Eq. 1-3, more so, the many mathematical steps of substitution and evaluation is eliminated with its use. Thus, Eq. 12 is a simple model which can be used at anytime to evaluate crack sizes, make design consideration, determine damage tolerance and identify safe operating or loading condition for Martensitic steel with edge and surface cracks without much recourse to many mathematical steps and processes.
CONCLUSION
The modeling of the constitutive relationship between crack lengths, numbers of fatigue cycles and constant amplitude stress for Martensitic steel containing edge and surface cracks have been done. The outcome of an experiment on high yield strength (σy = 100 Ksi (689 MN m-2), critical stress intensity factor (Kc) = 150 Ksi [in]1/2 (165 MN mm-2) Martensitic steel in air environment by Odukwe et al. (2007) was employed together with the relations for linear elastic fracture mechanics and the stress intensity factor range Eq. 1 and 3, to develop a working model which was used to generate data after substitution of the values of A and M together with the constant for edge and surface cracks. The desired crack lengths were inputted into it and corresponding number of fatigue cycles were generated. The result was then used to develop a novel model which can be used at any time to have access to data, make design changes and predict the behaviour of the metal to variable loading under specified amplitude stresses. This model, if used has removed the cumbersome mathematical processes involved in such data anlysis and also eliminates compulsory substitution which is required in previous models. It can also be used to predict crack sizes corresponding to desired number of fatigue cycles and amplitude stresses, by merely inputting right parameters; however it does not cover for all metals but for that used for the analysis.
REFERENCES
- De Los Rios, E.R., X.J. Xin and A. Navarro, 1994. Modelling microstructurally sensitive fatigue short crack growth. Proc. Math. Phys. Sci., 447: 111-134.
CrossRef - Navarro, A. and E.R. de Los Rios, 1992. Fatigue crack growth modelling by successive blocking of dislocations. Proc. Math. Phys. Sci., 437: 375-390.
CrossRef - Nelson, W., 1984. Fitting of fatigue curves with nonconstant standard deviation on data with runouts. J. Testing Evaluat., 12: 69-77.
CrossRef - Odukwe, O.A., O.O. Ajayi and G.O. Oluwadare, 2007. Simulation of crack growth rate in martensitic steel. J. Applied Sci., 7: 302-305.
CrossRefDirect Link - Pascual, F.G., Q. William and Meeker, 1999. Estimating fatigue curves with the random fatigue-limit model. Technometrics, 41: 277-290.
Direct Link - Sobczyk, K., 1987. Stochastic models for fracture damage of materials. Adv. Applied Probabil., 19: 652-673.
Direct Link - Tomkins, B., H.K. Grover and T.G.F. Gray, 1981. Subcritical crack growth: Fatigue, creep and stress corrosion cracking. Philosophical Trans. Royal Soc. London Series A Math. Physical Sci., 299: 31-44.
Direct Link








