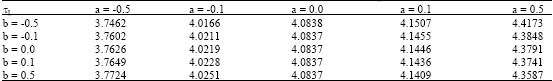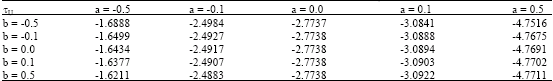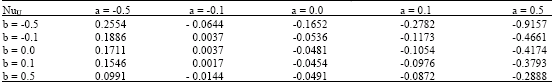Research Article
On the Effectiveness of Variation in the Physical Variables on the Generalized Couette Flow with Heat Transfer in a Porous Medium
Department of Mathematics, College of Science, AI-Qasseem University, P.O. Box 237, Buraidah 81999, Kingdom of Saudi Arabia