Submit Manuscript

Research Journal of Information Technology

Year: 2014 | Volume: 6 | Issue: 3 | Page No.: 207-215
Facebook Twitter Digg Reddit Linkedin StumbleUpon E-mail

ABSTRACT

In this study, RGB based image encryption was proposed. Initially the RGB components are separated, to each plane logistic mapping was employed. Then permutation was done for number of iterations given by the user and then the bitplanes are combined form a single image. Circular shift operation was performed on either left/right then up/down of the permuted pixels. As a final module, bitwise operation are applied based on two keys for row and column, respectively. To analyse the robustness of the proposed method correlation values, Unified Average Changing Intensity (UACI), Number of Pixels Change Rate (NPCR) and histogram tests were estimated.
PDF Abstract XML References Citation
Received: January 06, 2014;   Accepted: April 24, 2014;   Published: June 18, 2014

How to cite this article

Padmapriya Praveenkumar, G. Ashwin, S.P. Kartavya Agarwal, S. Naveen Bharathi, V. Suraj Venkatachalam, K. Thenmozhi and Rengarajan Amirtharajan, 2014. Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption. Research Journal of Information Technology, 6: 207-215.

URL: https://scialert.net/abstract/?doi=rjit.2014.207.215

INTRODUCTION

The place where mathematics and engineering meets can be called ‘cryptography’. It is one of the means by which a readable data or text is made unreadable (for the eavesdropper) by encrypting the readable data. A sender transforms an original text (plaintext) into a modified text (cipher text) by means of a cryptographic key using encryption. The receiver performs the reverse operation to retrieve back the original message by decryption. So, an interloper cannot tamper the concealed information. The remarkable cryptosystem services are confidentiality, legitimacy, access control, veracity and nonrepudiation. A good encryption method should thrive for two fundamental attributes, viz., confusion and diffusion (Diaconu and Loukhaoukha, 2013; Akhshani et al., 2012).

According to the keys used, cryptography can be classified as public key cryptography and private key cryptography. The two ciphers used in this mechanism are block ciphers and stream ciphers. In former, the operation is done on blocks of ciphers while in the latter operation is done bit by bit. The time taken for encryption and decryption is the disadvantage of cryptography (Amirtharajan and Rayappan, 2013). The effective solution to this problem will be ‘steganography’ (Amirtharajan and Rayappan, 2012a, b; Amirtharajan et al., 2013a-h; Ramalingam et al., 2014) and watermarking. “Steganography”-We can’t say that this sounds alien. It has been in use since very ancient times, term coined from Greek and is nothing but secret message in disguise, putting it simple, hidden writing. Now it is used in digitalized version. So, what exactly does it mean? The phenomenon by which one digit file is hidden or embedded in other. (Amirtharajan and Rayappan, 2013; Janakiraman et al., 2012; Padmaa and Venkataramani, 2014; Praveenkumar et al., 2012a, b, c, 2014a-k). Rajagopalan et al., 2012; Thanikaiselvan et al., 2012, 2013a, b; Thenmozhi et al., 2012).

Cryptography concept dates back to 2000 BC through hieroglyphics, an Egyptian practice. In modern world, cryptography has become a combat zone of top computer scientists and mathematicians. Because today, the decisive issue in business, online communication, war etc is the capability to safely hoard and transmit perceptive data. Cryptography is a significant classification of security system. It is characterized by plain text (original text), encryption (encoding), cipher text (modified text), decryption (decoding), key (tool with which plaintext is turned to cipher text).

Yang et al. (2010a) propose block encryption, universal modular transform with chaotic mapping to improve entropy and security. Luo et al. (2010) uses Lagrange’s equation on RGB plane to provide color image encryption. Huang and Zhang (2013) implements permutation based on six keys and utilizing chaotic maps to ensure encrypted image output. Amirtharajan et al. (2013a) reveals that how encryption can be applied to store secret information in a better way. Wireless communication with its enhanced efficiency, greater flexibility, mobility and reduced cost has encompassed human needs and sophistications to a greater extent. Several techniques adopted in the wireless standards solely contribute to its heightened demand.

Orthogonal Frequency Division Multiplexing (OFDM) is one such technique adopted to provide robust and high speed networks by countenancing signal overlap for secure communication using OFDM, steganography and encryption. Praveenkumar et al. (2014b) proposes image encryption in OFDM wireless environment to provide secure data transmission. A new chaos-based fast image encryption algorithm proposed and explained in (Kwok and Tang, 2007; Amin et al., 2010, Wang et al., 2011; Yang et al., 2010b; Xu et al., 2012) proposed a chaotic system based on circular bit shift and XOR operations. Ye (2010) gives out scrambling based on chaos Zhu et al. (2011) introduces bit-level permutation based on chaos combination. Yoon and Kim (2010) and Zheng and Gao (2011) introduce image encryption with permutation and chaotic maps.

Literature survey has been done on the existing RGB based image encryption algorithms. In this proposed methodology, to the individual bitplanes, logistic chaotic map has been applied to create shuffling. To the shuffled result, Rubik’s cube encryption process to get the final encrypted image. The next section provides the proposed methodology and followed section deals with results and discussion and finally section present the conclusion of this study.

METHODOLGY

In the proposed methodology, chatic logistic mapping was employed to the RGB planes of the original image to provide shuffling and Rubick’s cube encryption was employed on the shuffled image to get the final encrypted output. Figure 1 provides the block diagram of the proposed scheme.

Chaotic logistic mapping: The initial conditions and the system parameters are to be known to use any chaotic system. The chaotic map exhibits diffusion and confusion properties. Logistic mapping is a non linear polynomial dynamic mapping which has a degree of 2.

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption
Fig. 1: Proposed methodology

Rubik’s cube encryption algorithm:
Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption

Figure 2 represents the sequential operations performed in the Rubik’s cube principle in order to obtain the encrypted image.

As proposed in the algorithm circular shifts are performed on the individual rows and columns of the image matrix in order to obtain the maximum possible confusing over the original image. This way of rotating the rows and columns in right/left and up/down directions, respectively resembles the technique used to shuffle and solve the Rubik’s cube.

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption
Fig. 2: Block diagram of Rubik’s cube encryption

RESULTS AND DISCUSSION

This study was implemented on MATLAB 7.1 platform considering Lena, Baboon, camera man and peppers images of dimensions 256x256 in 8 bit format. Figure 3a provides the original Lena image, Fig. 3b provides the chaotic logistic map output after applying to R plane. Figure 3c provides the chaotic logistic map output after applying to G plane, Fig. 3d provides the chaotic logistic map output after applying to B plane. Figure 3e provides the combined output of R+G+B planes. Figure 3f provides the final encrypted Rubick’s cube output of the combined RGB plane. Figure 3g provides the histogram of the final encrytpted output and Fig. 3h provides the decrypted Lena image.

Figure 4a provides the original Baboon image, Fig. 4b provides the final encrypted output of Fig. 4a and c provides the histogram of Fig. 4b and d provides the decrypted output. Figure 5a provides the original cameraman image, Fig. 5b provides the final encrypted output of Fig. 5a and c provides the histogram of Fig. 5b and d provides the decrypted output. Figure 6a provides the original peppers image, Fig. 6b provides the final encrypted output of Fig. 6a and c provides the histogram of Fig. 6b and d provides the decrypted output. Table 1 provides the matrices like Horizontal, vertical, diagonal correlation values, NPCR and UACI of the final encrypted image with that of the original image.

NPCR and UACI: NPCR and UACI are the two metrices to estimate any encryption algorithm. They are considered to validate the pixel change rate and the average intensity change between the original and the encrypted image. Higher the values indicates that the proposed scheme reveals high resistance to differential and brute force attacks.

If A1 (i, j) and A2 (i, j) represents the pixel values in ith row and jth column of the two images XxY, respectively.

Then:

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption
Fig. 3(a-h):
(a) Original Lena image, (b) CL to redplane of Fig. 3a, (c) CL to green plane of Fig. 3a, (d) CL to blue plane of Fig. 3a, (e) Combined output of b+c+d, (f) Rubik’s encrypted output of Fig. 3e, (h) histogram of Fig. 3f, (g) Decrypted image *CL-Chaotic logistic map

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption
Fig. 4(a-d): (a) Original baboon image, (b) Encrypted output of Fig. 4a, (c) Histogram of Fig. 4b and (d) Secrypted image

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption

The propsed study provides NPCR and UACI values of 99.6 and 33.44, respectively.

Correlation analysis: In general, to examine the efficiency of the proposed cryptosystem, the correlation between adjacent pixels are calculated.

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption
Fig. 5(a-d): (a) Original cameraman image, (b) Encrypted output of Fig. 5a, (c) Histogram of Fig. 5b and (d) Decrypted image

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption
Fig. 6(a-d): (a) Original peppers image, (b) Encrypted output of Fig. 6a, (c) Histogram of Fig. 6b and (d) Decrypted image

Table 1: Image encryption matrices for various images
Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption

The correlation co-efficient ρ can be given by:

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption

where, x and y are adjacent pixels of the original images. To calculate the value of ñ the following discrete formulas can be used:

Image for - Rubik’s Cube Blend with Logistic Map on RGB: A Way for Image Encryption

where, I is the number of pixel pairs. From Table 1, the correlation values are nearing zero indicates that there exists no correlation between the original and the ciphered image.

CONCLUSION

In this study, chaotic logistic map on individual bit planes of RGB image followed by rubick’s encryption principle to provide the final encrypted image. Image encryption has become a combat zone of top computer scientists and mathematicians and encrypted image secret is safely hoarded and transmit. In this study, the computed horizontal, vertical and diagonal correlation values reveals that there exists no correlation between the original image and the shuffled image. The proposed encryption provides NPCR of 99.6, UACI of 33.5 and negative correlation values revels that resists against differential and brute force attacks.

REFERENCES

  1. Diaconu, A.V. and K. Loukhaoukha, 2013. An improved secure image encryption algorithm based on Rubik's cube principle and digital chaotic cipher. Math. Prob. Eng.
    CrossRefDirect Link
  2. Akhshani, A., A. Akhavan, S.C. Lim and Z. Hassan, 2012. An image encryption scheme based on quantum logistic map. Commun. Nonlinear Sci. Numer. Simul., 17: 4653-4661.
    CrossRefDirect Link
  3. Amin, M., O.S. Faragallah and A.A. Abd El-Latif, 2010. A chaotic block cipher algorithm for image cryptosystems. Commun. Nonlinear Sci. Numer. Simul., 15: 3484-3497.
    CrossRefDirect Link
  4. Amirtharajan, R. and J.B.B. Rayappan, 2012. Brownian motion of binary and gray-binary and gray bits in image for stego. J. Applied Sci., 12: 428-439.
    CrossRefDirect Link
  5. Amirtharajan, R. and J.B.B. Rayappan, 2012. Pixel authorized by pixel to trace with SFC on image to sabotage data mugger: A comparative study on PI stego. Res. J. Inform. Technol., 4: 124-139.
    CrossRefDirect Link
  6. Amirtharajan, R. and J.B.B. Rayappan, 2013. Steganography-time to time: A review. Res. J. Inform. Technol., 5: 53-66.
    CrossRefDirect Link
  7. Amirtharajan, R., P. Archana and J.B.B. Rayappan, 2013. Why image encryption for better steganography. Res. J. Inform. Technol., 5: 341-351.
    CrossRefDirect Link
  8. Amirtharajan, R., S. Sulthana and J.B.B. Rayappan, 2013. Seeing and believing is a threat: A visual cryptography schemes. Res. J. Inform. Technol., 5: 435-441.
    CrossRefDirect Link
  9. Amirtharajan, R., K. Karthikeyan, M. Malleswaran and J.B.B. Rayappan, 2013. Kubera kolam: A way for random image steganography. Res. J. Inform. Technol., 5: 304-316.
    CrossRefDirect Link
  10. Amirtharajan, R., M.V. Abhiram, G. Revathi, J.B. Reddy, V. Thanikaiselvan and J.B.B. Rayappan, 2013. Rubik's cube: A way for random image steganography. Res. J. Inform. Technol., 5: 329-340.
    CrossRefDirect Link
  11. Amirtharajan, R., S. Sulthana and J.B.B. Rayappan, 2013. Seeing and believing is a threat: A visual cryptography schemes. Res. J. Inform. Technol., 5: 435-441.
    CrossRefDirect Link
  12. Amirtharajan, R., K.M. Ashfaaq, A.K. Infant and J.B.B. Rayappan, 2013. High performance pixel indicator for colour image steganography. Res. J. Inform. Technol., 5: 277-290.
    CrossRefDirect Link
  13. Amirtharajan, R., V. Rajesh, P. Archana and J.B.B. Rayappan, 2013. Pixel indicates, standard deviates: A way for random image steganography. Res. J. Inform. Technol., 5: 383-392.
    CrossRefDirect Link
  14. Amirtharajan, R., P.S. Priya and J.B.B. Rayappan, 2013. Pixel indicated user indicator: A muxed stego. Res. J. Inform. Technol., 5: 73-86.
    CrossRefDirect Link
  15. Ramalingam, B., R. Amirtharajan and J.B.B. Rayappan, 2014. Stego on FPGA: An IWT approach. Sci. World J.
    CrossRefDirect Link
  16. Huang, F. and G. Zhang, 2013. A new image permutation approach using combinational chaotic maps. Inform. Technol. J., 12: 835-840.
    CrossRefDirect Link
  17. Luo, H., F.X. Yu, H. Li and Z.L. Huang, 2010. Color image encryption based on secret sharing and iterations. Inform. Technol. J., 9: 446-452.
    CrossRefDirect Link
  18. Janakiraman, S., R. Amirtharajan, K. Thenmozhi and J.B.B. Rayappan, 2012. Firmware for data security: A review. Res. J. Inform. Technol., 4: 61-72.
    CrossRefDirect Link
  19. Kwok, H.S. and W.K.S. Tang, 2007. A fast image encryption system based on chaotic maps with finite precision representation. Chaos Solitons Fract., 32: 1518-1529.
    CrossRefDirect Link
  20. Padmaa, M. and Y. Venkataramani, 2014. Adaptive data hiding based on visual cryptography. J. Applied Sci., 14: 1674-1688.
    CrossRefDirect Link
  21. Praveenkumar, P., R. Amirtharajan, Y. Ravishankar, K. Thenmozhi, J. Bosco and B. Rayappan, 2012. Random and AWGN road for MC-CDMA and CDMA bus to phase hide: A MUX in MUX stego. Proceedings of the International Conference on Computer Communication and Informatics, January 10-12, 2012, Coimbatore, India, pp: 1-6.
    CrossRefDirect Link
  22. Praveenkumar, P., R. Amirtharajan, K. Thenmozhi and J.B.B. Rayappan, 2012. Regulated OFDM-role of ECC and ANN: A review. J. Applied Sci., 12: 301-314.
    CrossRefDirect Link
  23. Praveenkumar, P., R. Amirtharajan, K. Thenmozhi and J.B.B. Rayappan, 2012. Phase for face saving-a multicarrier stego. Procedia Eng., 30: 790-797.
    CrossRefDirect Link
  24. Praveenkumar, P., R. Amirtharajan, K. Thenmozhi and J.B.B. Rayappan, 2014. Sub carriers carry secret: An absolute stego approach. J. Applied Sci., 14: 1728-1735.
    CrossRefDirect Link
  25. Praveenkumar, P., R. Amirtharajan, K. Thenmozhi and J.B.B. Rayappan, 2014. Double layer encoded encrypted data on multicarrier channel. J. Applied Sci., 14: 1689-1700.
    CrossRefDirect Link
  26. Praveenkumar, P., K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Purposeful error on OFDM: A secret channel. Inform. Technol. J., 13: 1985-1991.
    CrossRefDirect Link
  27. Praveenkumar, P., G.S. Hemalatha, B. Reddy, K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Secret link through simulink: A stego on OFDM channel. Inform. Technol. J., 13: 1999-2004.
    CrossRefDirect Link
  28. Praveenkumar, P., K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Stego in multicarrier: A phase hidden communication. Inform. Technol. J., 13: 2011-2016.
    CrossRefDirect Link
  29. Praveenkumar, P., K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Inserted embedding in OFDM channel: A multicarrier stego. Inform. Technol. J., 13: 2017-2021.
    CrossRefDirect Link
  30. Praveenkumar, P., K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Data puncturing in OFDM channel: A multicarrier stego. Inform. Technol. J., 13: 2037-2041.
    CrossRefDirect Link
  31. Praveenkumar, P., R. Deepak, K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Reversible steganography on OFDM channel: A role of cyclic codes. Inform. Technol. J., 13: 2047-2051.
    CrossRefDirect Link
  32. Praveenkumar, P., R. Deepak, K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Reversible steganography on OFDM channel: A role of cyclic codes. Inform. Technol. J., 13: 2047-2051.
    CrossRefDirect Link
  33. Praveenkumar, P., K. Thenmozhi, J.B.B. Rayappan and R. Amirtharajan, 2014. Spread and hide-a stego transceiver. Inform. Technol. J., 13: 2061-2064.
    CrossRefDirect Link
  34. Praveenkumar, P., R. Amirtharajan, R.S. Janani, K. Thenmozhi and J.B.B. Rayappan, 2014. Multi (Carrier+Modulator) adaptive system-an anti fading stego approach. J. Applied Sci., 14: 1836-1843.
    CrossRefDirect Link
  35. Rajagopalan, S., R. Amirtharajan, H.N. Upadhyay and J.B.B. Rayappan, 2012. Survey and analysis of hardware cryptographic and steganographic systems on FPGA. J. Applied Sci., 12: 201-210.
    CrossRefDirect Link
  36. Thanikaiselvan, V., P. Arulmozhivarman, J.B.B. Rayappan and R. Amirtharajan, 2012. Graceful graph for graceful security-towards a STE (G) Raph. Res. J. Inform. Technol., 4: 220-227.
    CrossRefDirect Link
  37. Thanikaiselvan, V., K. Santosh, D. Manikanta and R. Amirtharajan, 2013. A new steganography algorithm against chi square attack. Res. J. Inform. Technol., 5: 363-372.
    CrossRefDirect Link
  38. Thanikaiselvan, V., P. Arulmozhivarman, S. Subashanthini and R. Amirtharajan, 2013. A graph theory practice on transformed image: A random image steganography. Scient. World J.
    CrossRef
  39. Thenmozhi, K., P. Praveenkumar, R. Amirtharajan, V. Prithiviraj, R. Varadarajan and J.B.B. Rayappan, 2012. OFDM+CDMA+Stego = Secure communication: A review. Res. J. Inform. Technol., 4: 31-46.
    CrossRefDirect Link
  40. Wang, Y., K.W. Wong, X. Liao and G. Chen, 2011. A new chaos-based fast image encryption algorithm. Applied Soft Comput., 11: 514-522.
    CrossRef
  41. Xu, S.J., X.B. Chen, R. Zhang, Y.X. Yang and Y.C. Guo, 2012. An improved chaotic cryptosystem based on circular bit shift and XOR operations. Phys. Lett. A, 376: 1003-1010.
    CrossRefDirect Link
  42. Yang, X., X. Yu, Q. Zou and J. Jia, 2010. Image encryption algorithm based on universal modular transformation. Inform. Technol. J., 9: 680-685.
    CrossRefDirect Link
  43. Yang, H., K.W. Wong, X. Liao, W. Zhang and P. Wei, 2010. A fast image encryption and authentication scheme based on chaotic maps. Commun. Nonlinear Sci. Numer. Simul., 15: 3507-3517.
    CrossRefDirect Link
  44. Ye, G., 2010. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett., 31: 347-354.
    CrossRefDirect Link
  45. Yoon, J.W. and H. Kim, 2010. An image encryption scheme with a pseudorandom permutation based on chaotic maps. Commun. Nonlinear Sci. Numer. Simul., 15: 3998-4006.
    CrossRef
  46. Zheng, J.M. and W.Z. Gao, 2011. Color image encryption algorithm based on chaotic map. Comp. Eng. Des., 32: 2934-2937.
    Direct Link
  47. Zhu, Z.L., W. Zhang, K.W. Wong and H. Yu, 2011. A chaos-based symmetric image encryption scheme using a bit-level permutation. Inform. Sci., 181: 1171-1186.
    CrossRef

Related Articles

Tri Layer Image Encryption Based on Quantum Principle
Horse DNA Runs on Image: A Novel Road to Image Encryption
Image Merger Encryptor: A Chaotic and Chebyshev Key Approach
Chain of Shuffling and Chaos: A Tied Encryptic Approach
Light Weight Steganography on RISC Platform-Implementation and Analysis
Brownian Motion of Binary and Gray-Binary and Gray Bits in Image for Stego
Pixel Authorized by Pixel to Trace with SFC on Image to Sabotage Data Mugger: A Comparative Study on PI Stego
Steganography-Time to Time: A Review
Kubera Kolam: A Way for Random Image Steganography
High Performance Pixel indicator For Colour Image Steganography

Comments

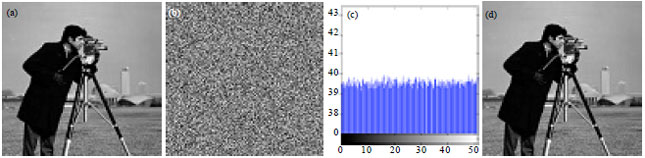
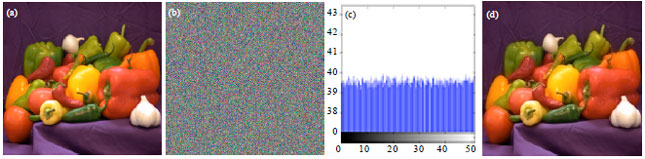
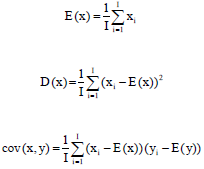
Hayat Ali Reply

can you help me please .. I want the Rubik program that you used in this article because I need it.
please help me

Leave a Reply

Your email address will not be published. Required fields are marked *