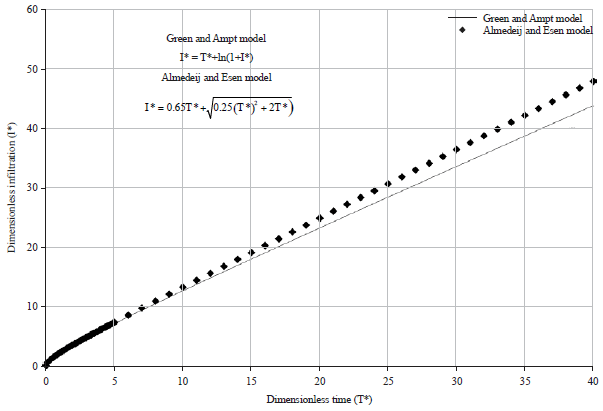
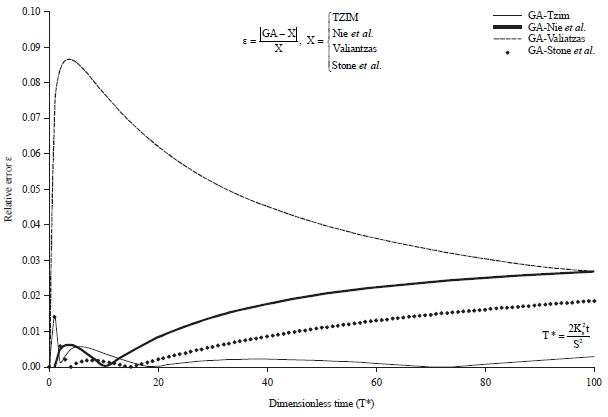
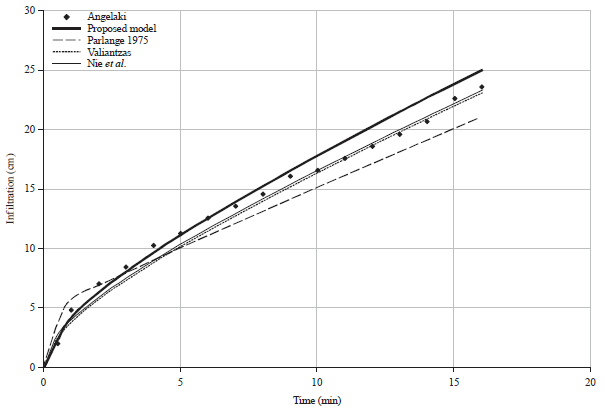
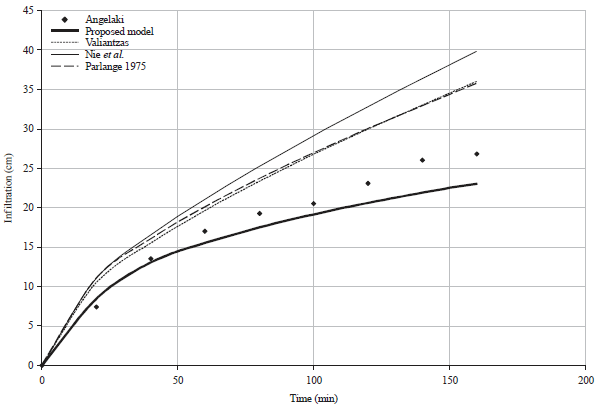
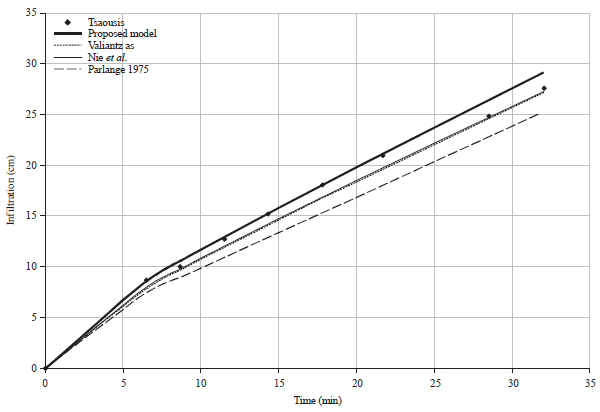
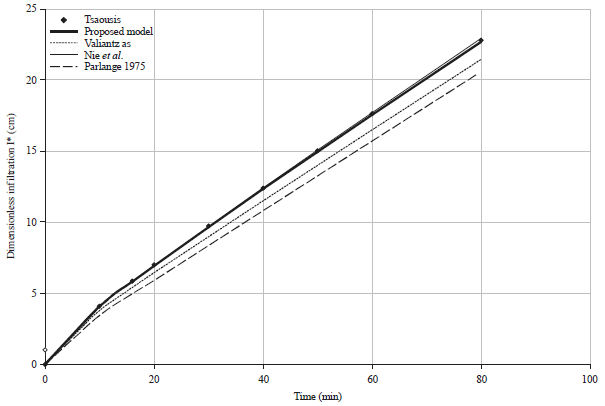
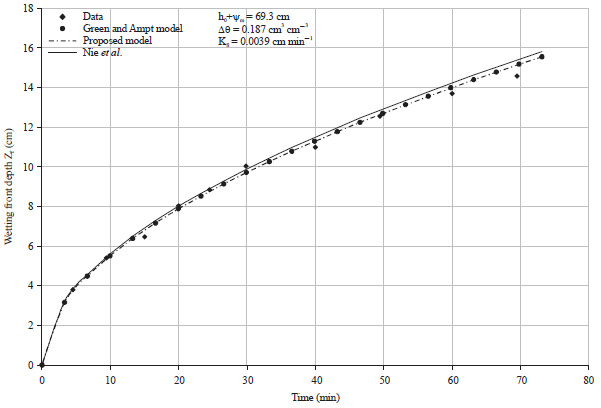
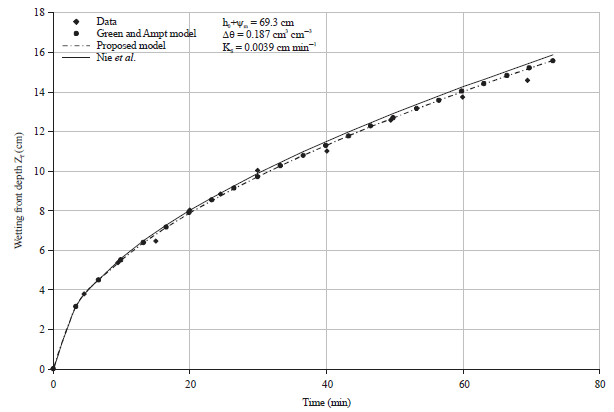
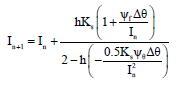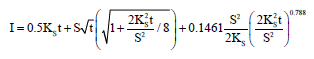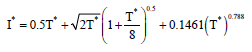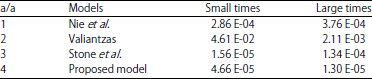Research Article
New Explicit Form of Green and Ampt Model for Cumulative Infiltration Estimation
Department of Rural and Surveying Engineering, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
LiveDNA: 30.767
Papaevangelou George
Department of Rural and Surveying Engineering, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
Papadopoulos Kyriakos
Department of Mathematics, Kuwait University, Khaldiya Campus, 13060 Safat, Kuwait
Evangelides Chris
Department of Rural and Surveying Engineering, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece