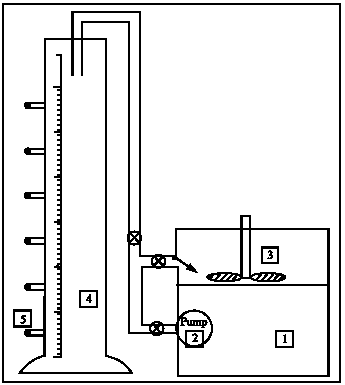
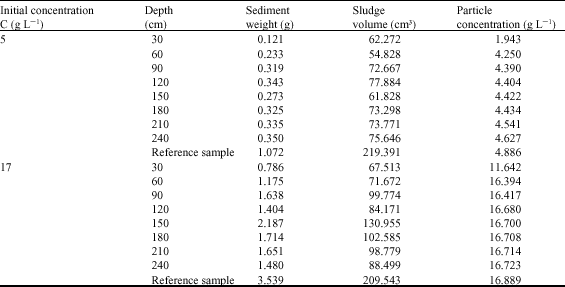
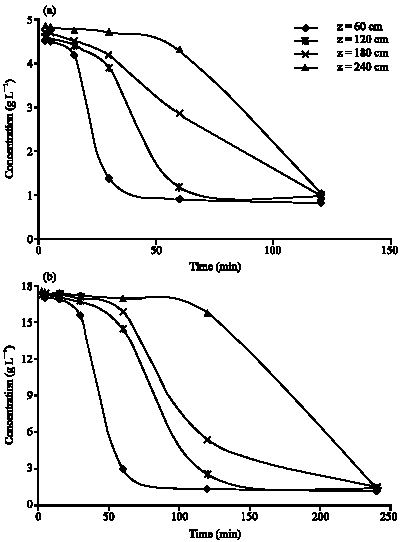
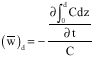Research Article
Fall Velocity of Cohesive Sediments in Dez Dam Reservoir
School of Water Sciences Engineering, Shahid Chamran University, Ahvaz, Iran
M. Fathi-Moghadam
School of Water Sciences Engineering, Shahid Chamran University, Ahvaz, Iran
H. Samadi
Department of Irrigation, Shahrekord University, Shahrekord, Iran
S. Emamgholizadeh
Department of Soil and Water, Shahrood University of Technology, Shahrood, Iran