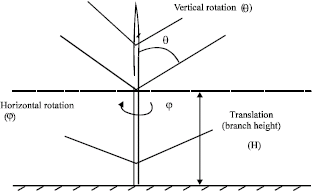
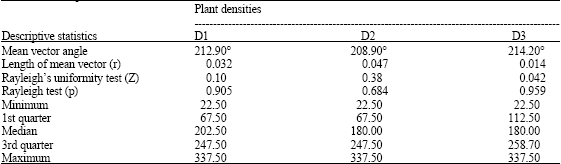
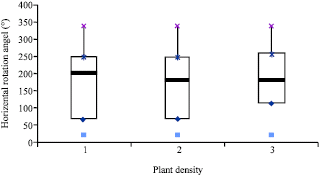
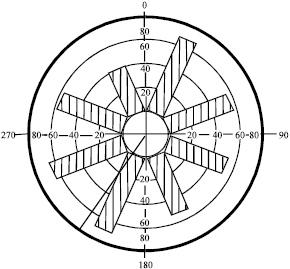
Research Article
Effects of Intra-Plant Competition on the Ensuing Spatial Branching Patterns of Straits Rhododenron
Institute of Biological Sciences, University of Malaya, 509603, Kuala Lumpur, Malaysia
B.B. Baki
Institute of Biological Sciences, University of Malaya, 509603, Kuala Lumpur, Malaysia
Shogo Kato
Institute of Statistical Mathematics, 4-6-7 Minami-Azabu, Minato-Ku, Tokyo 106-8569, Japan
K. Shimizu
Department of Mathematics, Keio University, 3-14-1 Hiyoshi, Kohoku-ku,Yokohama 223-8522, Japan
C.H. Sim
Institute of Mathematical Sciences, University of Malaya, 509603, Kuala Lumpur, Malaysia