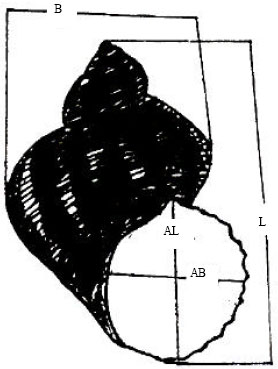
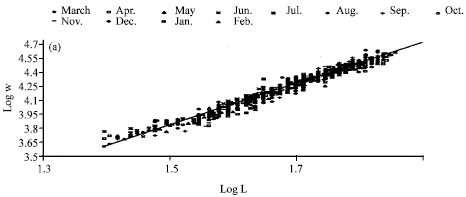
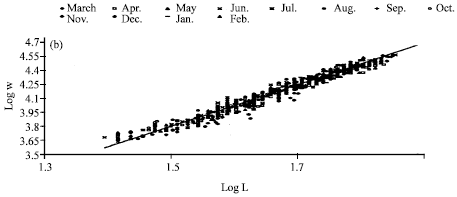
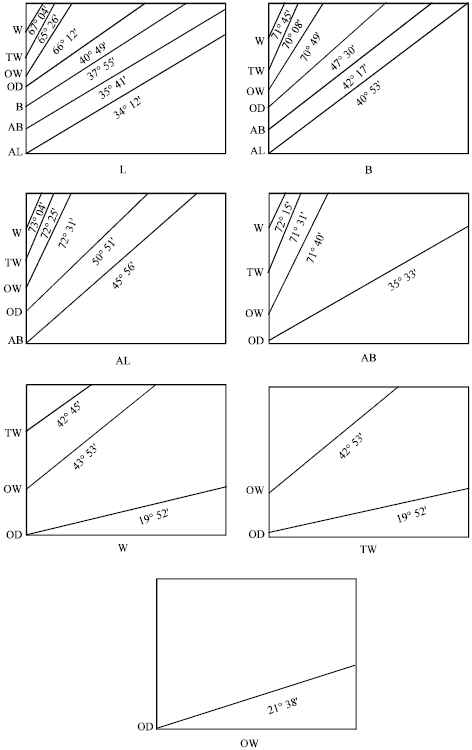
Research Article
A Statistical Approach on the Length-Weight Relationship and Allometry of Turbo brunneus
Noorul Islam College of Arts and Science, Kumaracoil-629180, India
S. Ravichandran
Centre of Advanced Study in Marine Biology, Annamalai University, Parangipettai-608502, India