Research Article
Predicting Up/Down Direction using Linear Discriminant Analysis and Logit Model: The Case of SABIC Price Index
Department of Quantitative Methods, School of Business, King Faisal University, Hofuf, Alhasa 31982, Saudi Arabia
Trading stock market indices has increased with economic growth due to the unprecedented popularity of major global financial markets. Financial forecasting in general and the stock market prediction in particular, has become an issue of interest to both the academic and the economic communities. Because these approaches are able to accurately forecast stock price movements and provide considerable benefits both to the firms and the investors. By nature, trading in index securities provide a less risk exposure to the markets and in particular have greater unsystematic risk hedging due to global diversification. There are two basic reasons for the success of these index-trading vehicles: Firstly, they provide an effective means for investors to hedge against potential market risks and secondly, they create new profit making opportunities for market speculators and arbitrageurs. Therefore, being able to forecast stock market indices accurately, these approaches have profound implications and significance for researchers and practitioners.
Traditionally, stock market prediction methods can be classified into two groups: technical (Murphy, 1998) and fundamental analysis (Ou and Wang, 2009). The former denotes a security analysis discipline for forecasting the direction of prices through the study of past market data, price and volume. Behavioral economics and quantitative analysis incorporate technical analysis in active management even though it violates the tenets of modern portfolio theory. Conversely, according to Ou and Wang (2009) fundamental analysis predicts stock markets using information concerning the activities and financial situation of each company. A fundamental analysis of a company typically focuses on the following three factors. (1) general economy (inflation, interest rates, trade balance, etc.), (2) Condition of the industry (price of related commodities, related stock prices, etc.) and (3) The condition of the company (P/E, book value, profit, etc.).
Financial markets are complex, non-stationary, noisy, chaotic, non-linear and dynamic systems (Leung et al., 2000). Many factors such as economic conditions, political situations, traders’ expectations, catastrophes and other unexpected events may cause fluctuations in financial market movement which hinder predictions of stock market prices and their direction. In response to such scenario, data mining (or machine learning) techniques were introduced and applied for financial predictions. Besides, several such methods including traditional time series, machine learning and technical stock analysis, etc. (Hellstrom and Holmstrom, 1998). Many researchers also proposed schemes and metrics for back-testing their predictions. They also applied data mining techniques for several specific markets (Ou and Wang, 2009; Leung et al., 2000). For example, Ou and Wang, (2009) used ten data mining techniques to predict movement of the Hang Seng index. They found that the support and the least square support vector machines were the best performers in their experiment. Leung et al. (2000) compared classification and level estimation models using S&P 500, UK FTSE 100 and Japan Nikkei 225 indexes with the conclusion that these classifications outperform level estimations. Other studies have used data mining for predicting several stock movements of both the Indian stock market and Nikkei 225 indexes (Choudhry and Garg, 2008; Huang et al., 2005). Yousef and Rebai (2007) successfully used the methods of linear programming for classification purposes. In an other study, neural networks were used for analyzing stock markets (Kara et al., 2011) where Yildiz et al. (2008) obtained good results evaluating the Turkish stock exchange. Pan et al. (2005) showed that neural networks are capable of using inter market information when forecasting a specific index. Another analytical method widely used in analysis of stock markets is logistic regression. Historical analysis of market efficiency was conducted by Seiler and Rom (1997). Zou and Kita (2012) demonstrated good performance of the Chinese stock index. Many researchers showed (Zhu and Li, 2010) contrast logistic regression with discrimination analysis. However, the results obtained were not sufficient to choose a better method from these two techniques. Most of the research suggests that the performance of logistic regression and linear discrimination analysis are similar (Zhu and Li, 2010; Pohar et al., 2004). This study investigated two data mining methods, namely LDA and LM, to predict day-by-day trends of SABIC. Also, predictions have been made for SABIC stock movement with and without considering the Saudi index.
SABIC AND STOCK PRICE MOVEMENT PREDICTION MODEL
SABIC corporation: The SABIC is one of the world’s leading manufacturers of chemicals, fertilizers, plastics and metals. The company supplies materials to other companies for developing products on which the world depends on its markets. The corporation is the largest and most reliably profitable public company in the Middle East with sound investor relations. SABIC's stock shares trade according to the defined rules set by the Saudi Stock Exchange (SSE) which is also known as TADAWUL.
There is a large amount of information that may affect SABIC share price; therefore, we have selected several factors based on significance and availability:
| • | Dow Jones Index (DJI): SABIC is a global corporation. Global economic conditions may directly affect SABIC. Therefore, we choose DJI, a representative of global economic conditions, as a factor for predicting SABIC movement |
| • | Crude oil price: SABIC products are petroleum based. Consequently, crude oil price affect its stock price |
| • | SABIC price data: This is a technical data that shows the trend of stock movement |
| • | Saudi index (optional): Since SABIC is a Saudi corporation, Saudi economic conditions which can be represented by the Saudi index, may significantly affect its stock price |
Stock price movement prediction model: The general model of stock price movements is defined as:
| (1) |
where, Dt is the direction of SABIC price movement at time t and is defined as categorical value “1” if the closing price at time t is greater than the closing price at time t-1; otherwise, it is defined as “0”, rsaudi is return of Saudi index at time t-1, roil is return of oil at time t-1, rDJI is return of DJI at time t-1, CSABIC is closing price of SABIC at time t-1, OSABIC is opening price of SABIC at time t-1, LSABIC is lowest price of SABIC at time t-1, HSABIC is highest price of SABIC at time t-1 and VSABIC is volume of SABIC at time t-1.
CLASSIFICATION VIA REGRESSION
Classification as a regression problem: The training data is represented by {(x1, y1),…, (xn, yn)} where:
X = (X1,…, Xp) |
Where, X denotes real-valued random input vector (independent variables, in our case-continuous variables) and Y is a response variable (dependent variable), denoting categories to which each observation belongs. Y is a categorical variable, i.e., Y ∈ {1, 2,.., K}.
The objective of the analysis was to obtain a predictor-function G(x) which has i as arguments and predicts values of Y. As Y denotes categories we can interpret G(x) as a function dividing the input space into a set of homogenous subsets. Each of them represents a different category from Y.
In the case of variable which is analyzed here, the response is binary. Hence, predictor G(x) divides space X in two classes and has the form of a hyperplane:
| (1a) |
where, x denotes input (independent) variables, β denotes coefficients and p denotes number of input variables.
Consequently, the two regions separated have values of G(X) greater than 0 and smaller than 0.
Let us now define Bayes’ classification rule. The training data {(x1, y1),…, (xn, yn)} are independent samples from the joint distribution of X and:
| (1b) |
We define the loss function of classifying Y as G(X) = ![]() as
as ![]() . The marginal distribution of Y is specified by probability py(y).The conditional distribution of X given Y = y is:
. The marginal distribution of Y is specified by probability py(y).The conditional distribution of X given Y = y is:
| (1c) |
The optimal classification rule should minimize the expected loss which can be defined as:
| (1d) |
Since X is independent, we can rewrite the right hand side of (4) as a sum. Consequently, minimizing the left hand side of (4) can be achieved by minimizing EX[E(Y|X)L(G(X),Y)]. for each X. Therefore, we receive the optimal classifier:
| (1e) |
As mentioned earlier, this study covers a binary response variable. For this type of variables, the loss function equals 1 for:
| (1f) |
When we put Eq. 1f into 1e, we obtain:
| (1g) |
Therefore, in case of binary response variables, the Bayes classification rule is as follows:
| (1h) |
which can be interpreted as a maximum a posteriori probability.
In this study, two algorithms were considered for classification i.e., LDA and Logistic Regression. For both the algorithms, Pr(Y = y|X = x) was estimated and then applied the Bayes rule G(X) = argminy Pr(Y = y|X = x). These algorithms were presented in the following sections.
Linear discriminant analysis (LDA): Consider a set of observations X for each sample of an object with known class Y. This can be designated as the training set. The classification problem is to find a predictor for the class Y of any sample of the same distribution given an observation X.
LDA assumed that the conditional probability density functions Pr(x|y = 0) and Pr(x|y = 1) and both are normally distributed with mean and covariance parameters (μ0, σ0) and parameters (μ1, σ1), respectively. Under this assumption, the Bayes’ optimal solution is to predict points as being from the second class if the ratio of the log-likelihoods is below some threshold T, so that:
| (2) |
LDA also makes the simplifying homoscedastic assumption (i.e., that the class covariances are identical, so σ0 = σ1 = σ) and that the covariances have full rank according to Ou and Wang (2009). In this case, several terms cancel and the above decision criterion becomes a threshold on the dot product:
| (3) |
for some threshold constant c, where:
| (4) |
This means that the criterion of an input X being in a class Y is purely a function of this linear combination of the known observations. It is often useful to see this conclusion in geometrical terms: the criterion of an input X being in a class Y is purely a function of projection of the multidimensional-space point x onto direction w. In other words, the observation belongs to Y if the corresponding X is located on a certain side of a hyperplane perpendicular to w and the location of the plane is defined by the threshold c.
Logit model: Researchers widely use Logistic regression as a statistical modeling technique when the target variable is categorical/binary with two categories. For example, buy stocks or do not buy. It can be used to predict a dependent variable on the basis of categorical, independent variables and to determine the percent of dependent variable variance explained by the independent variables. It performs the same task as LDA. However, there are some differences between these two models. The logistic model uses a sigmoid function that provides an output between 0 and 1 which makes it appropriate for financial studies on stock directions and bankruptcy. Another important difference is that logistic model uses a probabilistic method based on maximum likelihood with no distributional assumptions (normally distributed, linearly related or have equal variance in each group). Hence, it is assumed that logistic regression is more robust method with the given violations of these assumption. The model for logistic regression (Ou and Wang, 2009) is given as:
| (5) |
For two classes of output Y. We obtain β0, β1,…, βp, using the maximum likelihood approach.
Logit is given by:
| (6) |
The curves of π(X) are called sigmoid because they fit as S-shaped and, therefore, nonlinear curve to the data. The minimum for π(X) is attained at:
and the maximum for π(X) is obtained at:
Back-testing and hit-rate criterion: A crucial part of analysis involving statistical models is evaluating their accuracy. As models’ correctness in terms of lack of autocorrelation, hetereoscedasticity, colinearity is required for a good model it doesn’t guarantee its good performance which we assess iteratively. The usual way of assessing model’s accuracy is to compare its performance with historical data. Analyzing model’s accuracy is done for three main reasons: firstly, as a diagnostic of its potential for practical use. We assume that a model which has not been performant in the past will not perform well in the future. Because good performance in the past does not guarantee good performance in the future, however, it is more likely. Secondly, for analyzing model’s performance using historical data is to assess if a model’s density forecasts are statistically compatible with the realized values of the underlying random variable. Lastly, the model’s performance on historical data is the main criterion to rank alternative models and choose the most appropriate.
Hit rate criterion: The most common way to test model’s performance is back-testing. This compares values obtained from the model with historical (real) data. Again, we use the concept that a model that has been well-performing in the past is more likely to be well-performing in the future. An important issue is that back–testing gives a possibility to perform formal statistical tests of models’ accuracy and approximate risk of rejecting a correct model or accepting a false model.
This study predicted the direction of SABIC price movement Dt which is defined as a categorical value “1” if the closing price at time t is greater than the closing price at time t-1; otherwise, it was defined as “0”. Therefore, idea of back-testing was to compare Dt., real values of price movements, with ![]() , their predictions derived from the model. A simple measure which enabled us to quantify, assess and compare the performance of a model was a hit rate-summary statistic based on series of Dt and
, their predictions derived from the model. A simple measure which enabled us to quantify, assess and compare the performance of a model was a hit rate-summary statistic based on series of Dt and ![]() . The hit rate was computed as the ratio between the number of correct predictions, Dt. and the total number of moves in the stock time series:
. The hit rate was computed as the ratio between the number of correct predictions, Dt. and the total number of moves in the stock time series:
| (7) |
where, Dt is the prediction of ![]() computed at time t-1. The norm of the set in the definition is the number of elements in the set. Important advantages of the hit rate are its simplicity, natural interpretation and possibility to compare among different models. Moreover, it does not need any assumptions about the form of the model and its residuals etc. Hit rate is also a universal measure that can compare different types of models.
computed at time t-1. The norm of the set in the definition is the number of elements in the set. Important advantages of the hit rate are its simplicity, natural interpretation and possibility to compare among different models. Moreover, it does not need any assumptions about the form of the model and its residuals etc. Hit rate is also a universal measure that can compare different types of models.
Classification tables: Classification table is an extension of a simple hit rate. It allowed having a more detailed insight into models’ performance, analyzing sources of forecast errors. These displayed four types of combinations of observed and forecasted values: observed down, forecasted down (correct forecast), observed down, forecasted up (Type I-forecast error), observed up, forecasted down (Type II-forecast error), observed up, predicted up (correct forecast). Hence, they allowed us to analyze the cases the model performs better, if its performance is equilibrated, detect potential bias etc.
Wald test: Another way to verify quality of models’ forecasts is Wald’s test. This test was based on the comparison of observed (empirical) probabilities of events contrasted with theoretical (calculated) probabilities. Here, we define ‘event’ as growth of SABIC index.
The study tested:
where, ![]() denotes theoretical probability of event calculated from forecasts (number of cases where a given model forecasts growth of SABIC divided by the overall number of forecasts) and p0 denotes empirical probability calculated from the data (number of cases where the index has actually grown divided by the overall number of observations).
denotes theoretical probability of event calculated from forecasts (number of cases where a given model forecasts growth of SABIC divided by the overall number of forecasts) and p0 denotes empirical probability calculated from the data (number of cases where the index has actually grown divided by the overall number of observations).
The Wald’s test was based on the binomial distribution being approximated by normal distribution. Hence, the test statistic is follows:
which has a normal distribution.
Moreover, The Wald’s confidence intervals were calculated. If theoretical probabilities are inside of the Wald’s interval, the null hypothesis cannot be rejected which indicates correctness of forecasts. The formula for the Wald interval of confidence is below:
SIMULATION RESULTS AND DISCUSSION
The LDA and the LM were used to predict the movement of SABIC prices based on historical data of the DJI, oil price, Saudi index and SABIC price. The historical data were collected from the SSE, US Energy Information Administration and Yahoo finance website. Historical data for the DJI, crude oil, SABIC and Saudi index are shown in Fig. 1-4, respectively.
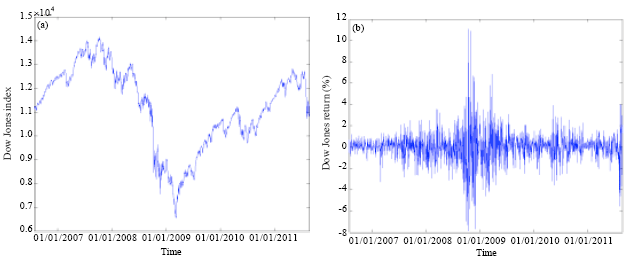 | |
| Fig. 1(a-b): | (a) Daily closing prices and (b) Return of DJI |
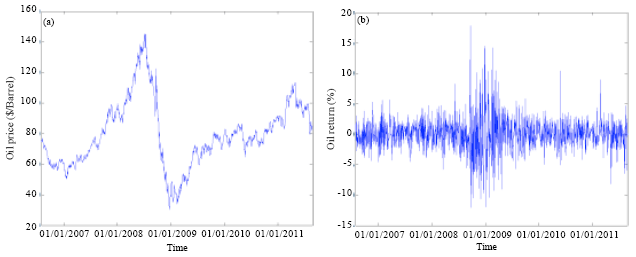 | |
| Fig. 2(a-b): | (a) Daily closing prices and (b) Return of oil |
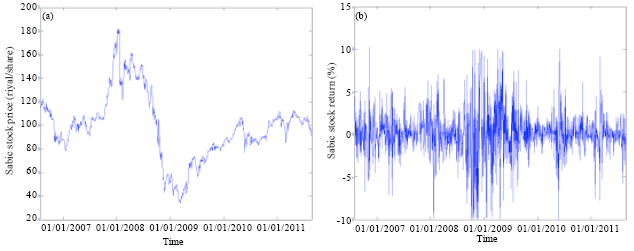 | |
| Fig. 3(a-b): | (a) Daily closing prices and (b) Return of SABIC |
 | |
| Fig. 4(a-b): | (a) Daily closing prices and (b) Return of the Saudi index |
The sampling period was from August 1, 2006 to August 24, 2011, thus making the sample a total of 1,267 trading days. The data was divided into two sub-samples where the in-sample or training data spans from August 1, 2006 to October 17, 2009 which included 800 trading days. The remaining data from October 18, 2009 to August 24, 2011 which included 467 trading days was reserved for out-of-sample or test data.
For each prediction method, we conducted two forecasts:
| • | With the Saudi index: Prediction based on the Saudi index, DJI, oil price and SABIC transaction information (high, low, open, close and volume) |
| • | Without the Saudi index: Prediction based on the DJI, oil price and SABIC transaction information (high, low, open, close and volume) |
LDA (with Saudi index): In this case, X = (rSaudi, roil, rDJI, CSABIC, OSABIC, LSABIC, HSABIC, VSABIC) with dimensions of p = 8 so that, eight coefficients of the LDA : VSABIC = 4.04, Voil = -5.89, VDJI = -9.06, VC = 0.094, VO = 0.082, VL = -0.053, VH = -0.12 and VV = -6.89x10-9. The in-and out-sample hit rates are shown in Table 1.
Coefficients of the discrimination function revealed the direction of relationships between explanatory (classification) variables and the dependent variable. A positive coefficient means that higher values of a given variable lead to higher probability of growth of the closing price in period t, a negative coefficient means that a higher value of a given variable is associated with higher probability of decline of the closing price in period t. Moreover, each coefficient value expresses the sensitivity of the prediction of the corresponding factor. For example, |VDJI|>|Voil| implies that a change in the DJI highly influenced the SABIC price direction than a change in oil price.
The most important factors of price movement of SABIC are the return of the DJI followed by the return of oil and Saudi index. Higher returns of DJI and oil price resulted in higher probability of a drop in closing price in period t. On the other hand, higher returns of Saudi index contributed to higher closing values of SABIC in period t. The coefficients of transaction data were much lower than the three first variables which means that their influence on price movements of SABIC was much lower (positive in case of opening and closing values; negative in case of high, low values and volume).
LDA (without Saudi index): In this case, X = (rSaudi, roil, rDJI, CSABIC, OSABIC, LSABIC, HSABIC, VSABIC) with dimensions of p = 7 so that, seven coefficients of the linear discriminant in Section 0 are obtained: Voil = -5.85, VDJI = -8.41, VC = 1.114, VO = 0.0598, VL = -0.045, VH = -0.127 and VV = -5.69x10-9. The in-and out-sample hit rates are shown in Table 1.
| Table 1: | Summary of back-testing-hit ratio results |
 | |
The coefficients [(V)]oil, VDJI, VC, VO, VL, VH, VV) correspond to w which is defined in (4). Basically, each coefficient value expresses the sensitivity of the prediction of the corresponding factor. For example, |VDJI|>|Voil| implies that a change in the DJI more greatly influences SABIC price direction than does a change in oil.
Again, the most important factors behind price movements of SABIC are returns of DJI and oil. The exercise negative influence over probability of a price growth of SABIC. Like in the first model transaction data are less important in predicting price changes of SABIC. Higher opening and closing values contributed to higher probabilities of a price surge of SABIC, higher lows, highs and volumes led to higher probabilities of a price decline.
LM (with Saudi index): In this case, X = (rSaudi, roil, rDJI, CSABIC, OSABIC, LSABIC, HSABIC, VSABIC) with dimensions of p = 8 so that, nine coefficients of the LM in Section 0 are obtained: β0 = -0.1875, βSaudi = -4.1433, βoil = 6.3760, βDJI = 9.4932, βC = -0.0965, βO = -0.0842, βL = 0.0552, βH = 0.1245 and βV = 6.6x10-9. The in-and out-sample hit rates are shown in Table 1.
It is difficult to interpret the numerical values of coefficients of the logistic regression directly. However, like in the LDA, their signs and compare absolute values of the coefficients can be interpreted. Negative sign means that higher value of a given explanatory variable contributed to higher probability of growth of closing price in period t. Greater absolute value of a coefficient indicated a more powerful influence of a given variable on the price change of SABIC.
Model coefficients, as shown above, revealed that the most powerful classification variables are return of DJI, return of oil and the return of Saudi index. Higher returns of DJI and of oil result in lower probability of a price growth of SABIC. The effect of returns of Saudi index is positive. Like in the LDA, transaction variables have less power in predicting the changes in SABIC prices. The influence of lows, highs and volumes on the probability of a price growth is negative while the influence of closing an opening values is positive (these result in higher probability of price growth of SABIC).
LM (without Saudi index): In this case, X = (roil, rDJI, CSABIC, OSABIC, LSABIC, HSABIC, VSABIC) with dimensions of p = 7 so that, eight coefficients of the LM in Section 0 are obtained: β0 = -0.1735, βoil = 6.3022, βDJI = 8.8866, βC = -0.1172, βO = -0.0612, βL = 0.0471, βH = 0.1301 and βV = 5.3x10-9. The in-and out-sample hit rates are shown in Table 1.
The coefficients β↓0, β↓oil, β↓DJI, β↓C, β↓O, β↓L, β↓H, [(“β”)]↓V) correspond to β which is defined by Murphy (1998). Basically, each coefficient value expresses the sensitivity of the prediction on the corresponding factor. For example, |βDJI|>|βoil| implies that a change in the DJI will highly influence SABIC price direction than does a change in oil. Again, the most powerful influence on the probabilities of price growth of SABIC are exercised by returns of DJI and oil. In their classification power, they outperformed transaction data. Higher returns of DJI and oil resulted in lower probability of a price growth of SABIC. Signs of coefficients for transaction data did not change after excluding the Saudi Index. Influence of lows, highs and volumes on probability of a price growth is negative while the influence of closing an opening value is positive.
The results of all the four models employed for analysis of SABIC index were consistent and revealed the same logic that the returns of oil and DJI are the most powerful factors for changes of SABIC index. Their influence was negative, i.e., their higher returns bring lower probabilities of SABIC growth. However, the transaction data proved less powerful in forecasting the changes in prices of SABIC.
The results showed that these two methods performed differently depending on in-or out-of samples. LDA gave a better hit rate for Out-sample with or without Saudi Index. While, LM gave a better hit rate for In-sample with or without considering Saudi index. These results are in close agreement with the results obtained by Zou and Kita (2012) using Bayesian network . In their study, the average correct answer rate was about 60%.
Furthermore, all the four models were analyzed for performance using classification presented in Table 2 and 3.
The analysis of classification tables provided us with some interesting information about model’s performance.
First of all, adding or excluding Saudi index does not change forecasts qualitatively. Sources of forecasts errors remain the same with and without Saudi index.
Another, interesting observation was that LDA and LM models performed differently-LDA models seem to produce more equilibrated forecast. In classification tables for the LM models, one can observe, that the models tended to predict down in many instances of up (35-36%). On the other hand, very often it predicted ‘Up’ for observed ‘Down’. This might be a valuable information when using models for investment purposes.
Wald test: Accuracy of forecasts were checked using the Wald test. Its results (test statistics, theoretical probabilities, intervals) are shown in Table 4. The critical value at 5% level of significance (0.05) is equal to 1.96 (two-tailed alternative hypothesis).
| Table 2: | Classification table for LDA |
 | |
| Values in brackets are numbers | |
| Table 3: | Classification table for LM |
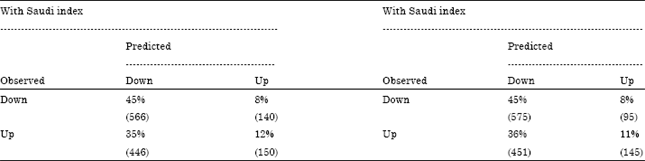 | |
| Values in brackets are numbers | |
| Table 4: | Summary of wald test |
 | |
For all the four model versions, the absolute value of test statistic is significantly higher than the critical value. Hence, in all the cases, the null hypothesis was rejected and accepted the alternative hypothesis-probabilities of growth derived from all the models significantly differed from the empirical probabilities. All the four models tended to underestimate probabilities of growth of the analyzed index.
The study utilized two classification techniques (LDA and LM) to forecast the daily movement of SABIC stock prices. The forecast was based on the DJI, oil price, Saudi index and historical transaction data of SABIC because they significantly affect SABIC price. From our simulation results, it was observed that it is very difficult to accurately predict stock price movement. Correct prediction of stock price direction ranged from 54.7 to 59.2%. The classification tables revealed different distribution of errors between logistic regression and linear discriminant analysis. Logistic regression tended to underestimate probabilities of growth of SABIC. The Wald’s test confirmed that there are statistically significant differences between predictions and real data. LDA scored better than LR. However, the predictions obtained may serve as good indicators for aiding investors in deciding their trading strategy. The results obtained are very useful and the trained data might be used routinely to generate daily predictions on the SABIC stock price in our real-money stock and index future trading. Currently, many “intelligent” data mining techniques such as neural network and machine learning methods are available which are the potential candidates for future testing.