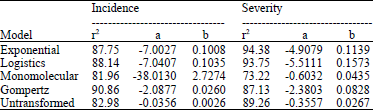
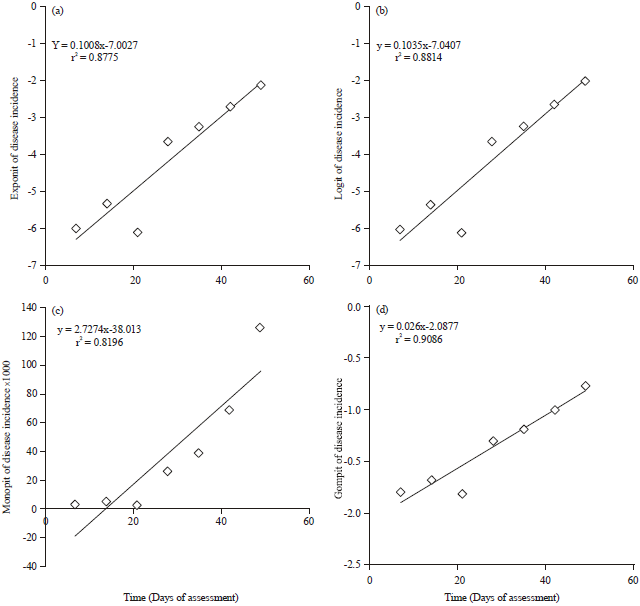
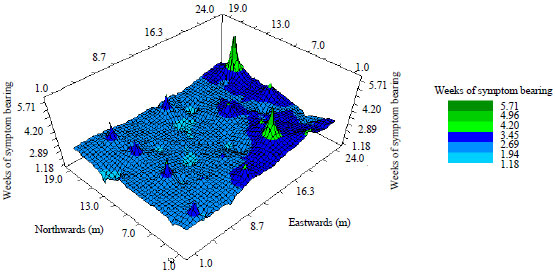
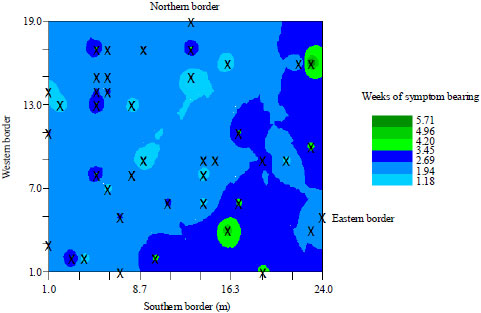
Research Article
Spatial and Temporal Spread Patterns of Viral Diseases on a Zucchini Squash Field in the Coastal Savannah Zone of Ghana
Department of Nuclear Agriculture and Radiation Processing, Graduate School of Nuclear and Allied Sciences, University of Ghana, P.O. Box AE1, Atomic, Accra, Ghana
H.M. Amoatey
Department of Nuclear Agriculture and Radiation Processing, Graduate School of Nuclear and Allied Sciences, University of Ghana, P.O. Box AE1, Atomic, Accra, Ghana
G.K. Owusu
Department of Nuclear Agriculture and Radiation Processing, Graduate School of Nuclear and Allied Sciences, University of Ghana, P.O. Box AE1, Atomic, Accra, Ghana