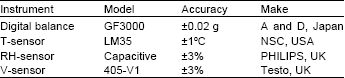
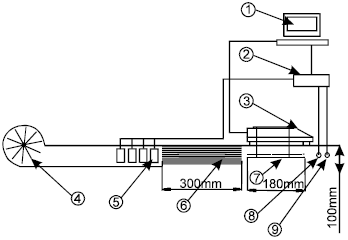
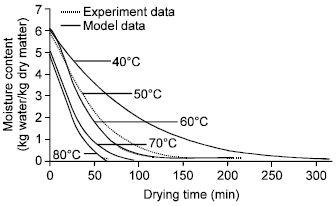
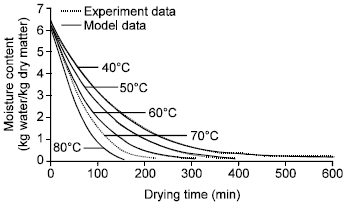
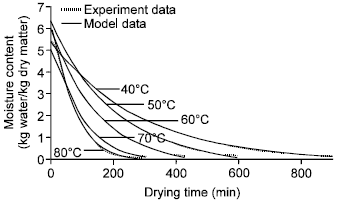
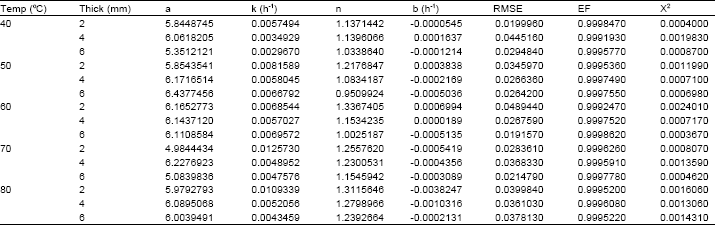
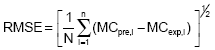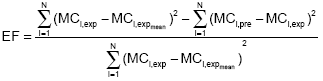Research Article
Mathematical Modeling of Moisture Content of Apple Slices (Var. Golab) During Drying
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran
Shahin Rafiee
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran
Alireza Keyhani
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran
Ahmad Tabatabaeefar
Department of Agricultural Machinery Engineering, Faculty of Biosystems Engineering, University of Tehran, Karaj, Iran