Research Article
Mapping Quantitative Trait Loci Using the Marker Regression and the Interval Mapping Methods
Department of Crop Science and Production, Botswana College of Agriculture, P/Bag 0027, Gaborone, Botswana
Quantitative genetic studies, including the use of Quantitative Trait Locus (QTL) mapping techniques, provide an opportunity to investigate the underlying genetic mechanisms that regulate developmental programs in plant architecture. QTL mapping studies provides the plant breeder with knowledge on how many genes govern a given character, what effect individual genes have, how these genes interact, how heritable they are and what impact the environment has on the trait. Once the genes have been identified this can help the breeder to select for such genes based on the gene`s linkage to specific markers. Weinig et al. (2002) observed that QTL mapping studies can provide important information about the genetic basis of life history evolution in natural population.
QTL mapping is done by looking for associations between the quantitative trait and the marker alleles segregating in the population (Zhi-Hong et al., 2005; Wang et al., 2007). A number of statistical approaches can be used to identify associations between the trait and particular markers, the technique used depending on the type of population. A strong association between the genotype at a marker locus and difference in the trait score indicates that there is a QTL in the vicinity of the marker. The statistical power of the approach will depend on the heritability of the trait and the size of the individual QTL effects, but it is now accepted that there is generally a very large confidence interval associated with the location of individual QTL. Some of the statistical methods used to map QTLs are; single marker analysis (Edwards et al., 1987), marker regression (Kearsey and Hyne, 1994), multiple regression (Haley and Knott, 1992), interval mapping (Lander and Botstein, 1989) and composite interval mapping (Jansen, 1996).
In this study, the interval mapping and marker regression methods were used for QTL detection. The interval mapping method uses an estimated genetic map as the framework for the location of the QTL. The intervals that are defined by ordered pairs of markers are searched and statistical methods are used to test whether a QTL is likely to be present within the interval or not. The results of the tests are expressed as logarithm of the odds (LOD) scores, which compare the evaluation of the likelihood function under the null hypothesis (no QTL) with the alternative hypothesis (QTL at the testing position) for the purpose of locating probable QTL (Doerge, 2002). The approach of interval mapping considers one QTL at a time and this can bias identification and estimation of QTL when multiple QTL are located in the same chromosome (Zeng, 1994).
The marker regression method of Kearsey and Hyne (1994) tries to locate the QTL with respect to all markers simultaneously by regression onto marker means. The method estimates the additive and dominance effects, tests their significance and tests for more than one QTL. The method is as reliable as the interval mapping and multiple regression approaches, but has wider application and is capable of hypothesis testing. However, because you do not know which markers flank the QTL or that there is just one QTL per chromosome, the marker regression approach does provide an overall test of the model, no matter how the QTLs are organised on the chromosome. The study compares QTL detection using the marker regression and the interval mapping methods.
MATERIALS AND METHODS
Plant material: The experiment was conducted at the University of Birmingham, United Kingdom between 2001 and 2003. The experimental material was produced by hand crossing the Arabidopsis ecotypes Columbia with Landsberg erecta to produce the F1. The F1 cross was verified by microsatellite (SSR) analysis. The verified F1 plants were self-pollinated to generate F2 plants and the F2 plants were evaluated for QTL using the marker regression and interval mapping methods.
Growth conditions: The plants were sown in the growth room in 7.5 cm pots containing soil mix of 2 parts John Innes No. 1 compost, 2 parts peat based compost and 1 part silvaperl. Three seeds were sown per pot and pots were placed on benches with perforated matting for underneath watering. Guard plants to minimize edge effects surrounded the experiment. The plants were exposed to 16 h photoperiod and 24°C temperature in the growth room. After two weeks, the seedlings were thinned to one per pot. Each plant was evaluated for height at 20 days after planting (HT20), cauline leaves at 20 days after planting (CL20) and at flowering (CLF), rosette leaves at 20 days after planting (RL20) and at flowering (RLF), time to produce flower buds (TTB), time to flower (TTF), height at flowering (HTF) and at 34 days after planting (HT34).
QTL analysis: Thirty microsatellite markers or simple sequence repeats (SSRs), chosen to cover the Arabidopsis genome at intervals of approximately 20 cM served as the basis for the QTL analysis. The markers covered approximately 513.10 cM of the Arabidopsis genome. Significant associations between specific markers and morphological traits detected by the marker regression and interval mapping methods were first confirmed by the single factor analysis of variance using the QTL cafe program that is available on the web (http:\\web.bham.ac.uk\g.g.seaton\) .
The marker regression method by Kearsey and Hyne (1994) estimates QTL position and the QTL effects. This essentially involves regressing the additive difference between marker genotype means at a locus against a function of the recombination frequency between that locus and a putative QTL. Considering the F2 plants as in this case, with two pure breeding parental lines of P1 (Columbia) and P2 (Landsberg). Suppose R represents the recombination frequency between the marker, M and the QTL, Q. ![]() can be defined as the mean value, of all the progeny whose marker genotype is M1M1, for the trait concerned. Via standard theory, an expression relating
can be defined as the mean value, of all the progeny whose marker genotype is M1M1, for the trait concerned. Via standard theory, an expression relating ![]() to the mid-parent (m), additive effect (a) of the QTL and the recombination frequency between the QTL and the ith marker locus (Ri) can be created:
to the mid-parent (m), additive effect (a) of the QTL and the recombination frequency between the QTL and the ith marker locus (Ri) can be created:
| |
| Via similar logic, |
| |
| Nowi, di is defined as the difference between the mean trait values for the two marker genotypes: |
| |
| di is half the difference between the means at the ith marker, Hence: |
| di = (1-2Ri)a |
| This gives a clear expression relating di, half the difference between the phenotypic effects of the two marker genotypes and a and Ri, the additive genetic effect of the QTL and the recombination frequency between a marker and the QTL, respectively. This relationship can be expressed as the equation of a straight line |
| di = (1-2Ri)a+0 |
| y = x.m+c |
di is represented on the y-axis, (1-2Ri) is plotted on the x-axis, the additive genetic effect of the QTL, a, is calculated from the gradient of m, when the intercept of the y-axis, c, is zero (Burns, 1997).
The positions of each marker are known, so the recombination frequency between each marker and the putative QTL position can be calculated and the results represented on a graph. Because the intercept of the y-axis is zero, the uncorrected part of the sum of squares can be used to calculate the regression items. This is a special case of regression analysis and alters the values of the items in the regression analysis of variance, as the correction term is effectively zero (Burns, 1997; Kearsey and Hyne, 1994).
At the correct position of the QTL, there is a simple linear regression of di onto (1-2Ri) with gradient a, which passes through the origin of the x and y-axis. The regression sum of squares item confirms that the additive effect (a) is not zero. This indicates that a significant difference exists between the mean trait values for the marker genotype classes at the locus concerned. The residual sum of squares item shows the model is adequate to explain the observed results: in this case, a one QTL per chromosome model. The most likely position of the QTL is where the residual sum of squares is minimal. The marker regression method is equally applicable to other generations derived from the F1 e.g., backcrosses, double haploids or single-seed descent lines (Kearsey and Hyne, 1994). The method provides a simple test for whether the QTL, located on a given chromosome in different populations, are the same and this is achieved through joint regression analysis. In this study, a QTL was assumed present when the probability (p) value associated with the regression was below 5%. If the residual was significant (p<1%) it was assumed that one QTL did not adequately explain the variation and a second QTL was added to the model.
The interval mapping method tested sequentially along each chromosome whether intervals flanked by two molecular markers contain a QTL while statistically accounting for other QTL segregating outside the tested interval. In this study, a 1 and 5 cm scan window was used when the distance between the markers was less than 20 and 50 cM respectively. The location of the maximum LOD profile was taken to indicate the location of the QTL. An LOD score greater than 2 was used to declare the presence of a QTL within a marker in this study (Lander and Botstein, 1989). The confidence intervals were set at the map interval corresponding to a 1 LOD decline either side of the peak (Lander and Botstein, 1989;Haley and Knott, 1992; Zeng, 1994).
Significant genetic variation measured by the F-statistic was observed in RL20, TTB, HT34, RLF, CLF, HTF and TTF, indicating that at least one or more QTL were segregating for the traits. The marker regression method detected 22 QTL in six traits, whereas the interval mapping method detected 22 QTL in seven traits. Figure 1 shows the QTL detected by each method and those detected by both methods. Sixteen QTL were detected by both the interval mapping and the marker regression methods and they mapped to similar positions of the chromosomes (Fig. 1, Table 1). QTL for different traits were sometimes mapped to similar regions of the chromosomes and this may suggest the same gene maybe involved in the control of the traits.
The QTL detected by the marker regression and the interval mapping method showed similar mode of additive
| Table 1: | Comparison between QTL detected using interval mapping and marker regression methods in the F2 plants |
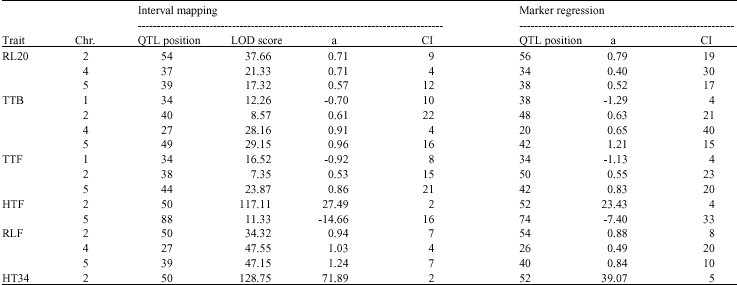 | |
| Chr. = Chromosome; LOD = Logarithm of the Odds; a = Additive effect; CI = Confidence interval | |
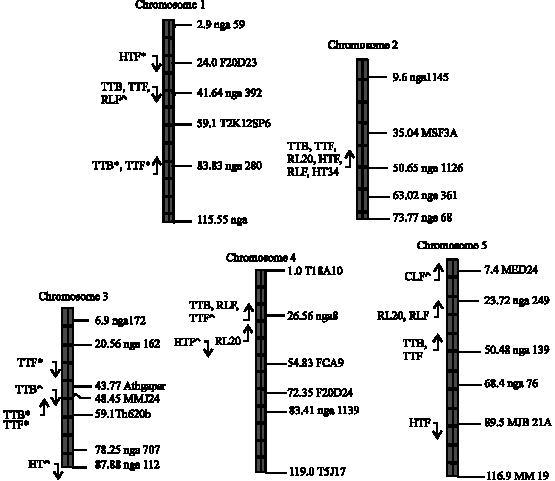 | |
| Fig. 1: | The location of QTL detected by the marker regression and interval mapping methods on Arabidopsis chromosomes, with those detected by both methods without any sign and those detected by the marker regression and interval mapping methods only indicated by the signs * and ^ respectively. The direction of additive effect is shown by the arrow |
effect, (Fig. 1, Table 1). The additive effect indicates the direction of the parent with the increasing or decreasing effect. In the QTL detected by both methods the direction of the additive effect was consistent with the difference between the parents, except for HTF in chromosome 5. For example, the QTL detected at chromosome 2 for TTB and TTF showed an increasing effect for the Columbia parent, indicating that the Landsberg parent decreased the time to produce buds and the time to flower and this is consistent with the difference between the parents since the Landsberg parent flowered earlier than the Columbia parent. There were very few QTL in which the direction of the additive effect was not consistent with the difference between the parents. Lynch and Walsh (1997) also observed that the direction of allele effects were not consistent with the direction of the difference between parental lines.
The QTL positions for TTF mapped to similar positions and showed similar mode of action as the QTL for time to produce flower buds (TTB). This is expected as the time to produce buds marks the beginning of the flowering period. QTL for rosette leaves also mapped to similar regions of the chromosomes. Figure 2 shows the QTL for HTF detected by the interval mapping method and the marker regression methods at approximately 50 cM. In both methods the peak determined the position of the QTL and in this case it indicates that indeed a QTL is present in chromosome 2 at around 50 cM.
The QTL for HT34 and HTF detected on chromosome 2 showed the highest LOD scores of 128.75 and 117.11 respectively and they also showed the highest additive effect (Table 1). Other QTL mapping to this position includes RL20, RLF, TTB and TTF detected by the marker regression and interval mapping methods. This QTL is likely to be the erecta mutation, which affects inflorescence architecture (Ungerer et al., 2002). The erecta mutation is not a naturally occurring mutation, but was generated in the laboratory through mutagenesis. Overall, the largest proportion of QTL detected was relatively of small effect. This result is consistent with
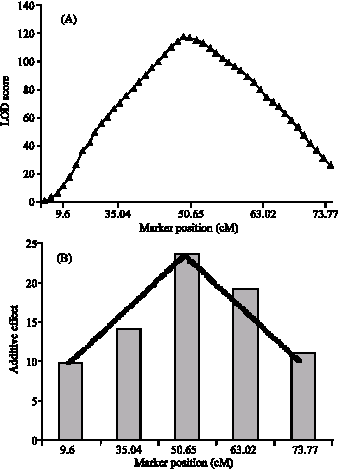 | |
| Fig. 2: | QTL for HTF detected at the same positions using interval mapping (A) and marker regression (B) methods at around 50 cM in chromosome 2 of Arabidopsis |
findings of other QTL studies documenting that most differences between lines are due to a small number of QTL of large effect accompanied by a large number of QTL of smaller effect (Lynch and Walsh, 1997). The apparent decline of QTL in the class of smallest effect should not be interpreted as evidence that small effect QTL are rare, but rather simply reflects the statistical difficulties of detecting these loci (Ungerer et al., 2002).
The 95% confidence interval for QTL detected using the interval mapping ranged from 2-25 cM, whereas that associated with marker regression ranged from 4-40 cM. In this experiment, the experimental size of 200 plants was used and this may have led to the higher confidence intervals. Van Ooijen (1992), Darvasi et al. (1993) and Kearsey and Farquhar (1998) have observed that the confidence limits and the reliability of the QTL studies can be improved by increasing the family size and the number of families. Kearsey and Pooni (1996) also stated that the precision of QTL position depends more on the population size than the number of markers and no notable increase in accuracy is obtained with more than five well spread markers for each chromosome. Therefore, it is important to use a mapping population of relatively large size and QTL of high heritability for reliable estimation of QTL effect.
The QTL mapping methods have evolved from simple t-test, single or multiple regressions to one-QTL models such as the interval mapping and composite interval mapping and further to the multiple-QTL models such as the multiple interval mapping. In practice, the detected QTL can be used for selecting parents with desired genotypes for producing progeny or gene transfer to achieve the ultimate goal of trait improvement in later generations. QTLs need to be mapped as precisely as possible to ensure good quality of the follow-up operation on QTL. Therefore, precision and unbiasedness in estimating the parameters of QTL should be more important than the ease of computation and implementation in QTL mapping (Kao et al., 1999). The methods of interval mapping and marker regression approach follow the procedure of creating a QTL model for the observed data and then testing that model for its suitability. In both cases the models are relatively simple and consider only one or two QTL thus giving a limited number of possibilities to be considered.
The interval mapping method and marker regression does not include the analysis of other parameters such as epistasis. When epistasis is included the range of possible models to be tested becomes much larger and the process of model selection and testing becomes extremely demanding (Doerge, 2002). The advantages of the marker regression over the interval mapping method are its ability to test for the presence of more than one QTL and the method incorporates all marker information on a chromosome in a single test (Hyne and Kearsey, 1995). In this study, the marker regression method detected two QTL for the same trait in chromosome 1 for TTF and TTB and chromosome 3 for TTF. In such cases the additive effect for the QTL had opposite signs and thus their effect canceled each other and this supports the biometric evidence for gene dispersion in the parents and this is in agreement with the findings of Hyne and Kearsey (1995). From the study it can be concluded that the methods of interval mapping and marker regression are very similar in their QTL detection even though the methods employed different techniques and significant levels.