Research Article
A Yield Prediction Model for Crimean Pine Plantations
Faculty of Forestry, Karadeniz Technical University, 61080 Trabzon, Turkey
Nuray Misir
Faculty of Forestry, Karadeniz Technical University, 61080 Trabzon, Turkey
Crimean pine (Pinus nigra subsp. pallasiana) is one of the most important both plantation and natural species in Turkey. Large scale plantations of crimean pine in Turkey were established in 1955. These plantations are estimated to about cover 500,000 hectares. Thus, it is important to develop growth and yield models for these areas to provide long-term decision making in forest management. Crimean pine has importance in Turkey for ages as a source of electric transmission poles for the rural electrification project and mine poles. Apart from electric and transmission poles and mine poles, it is also valued by local communities as poles for construction, fuel wood and wind breaks.
Growth and yield models, in general, constitute recruitment, growth and mortality models. They have traditionally been classified as stand models, individual tree models and diameter class models (Mısır, 2003). Individual tree models are further classified as distance-dependent (spatial) or distance-independent (non-spatial) models. Spatial models include a spatial competition measure. Competition is often expressed as a function of the distance between the subject tree and its neighbours as well as the size of the neighbours. Non-spatial models do not use spatial information to express competition, but they can use predictors (for example, stand basal area, mean diameter) which are measures for stand density and thus express overall competition in a stand (Pukkala, 1988; Vanclay, 1994; Laar and Akça, 1997).
Diameter class models simulate several classes of trees and are a compromise between stand models (one class) and individual tree models (a class for each individual). The stand need not be partitioned into metric classes (e.g., 10 cm dbh classes); a more flexible partition may be used (e.g., cohorts, or groups of trees with similar species, size and other characteristics) (Vanclay, 1995). Stand models often estimate growth and yield in terms of volume. They may also project values of other stand parameters such as basal area, mean diameter, height and number of trees per hectare. On the other hand, these are yield tables. A yield table presents the anticipated yields from an even-aged stand at various ages and is one of the oldest approaches to yield estimation. Normal yield tables provide estimates of expected yields tabulated by stand age and site index for ideal, fully stocked or normal forest stands. Yields were generally tabulated by age and site index but could also be presented as alignment charts. Normal yield tables may provide reliable estimates of potential yields for even-aged stands similar in character to those used in developing the table, but may be less satisfactory for natural stands where age may vary considerably within stands.
The objective of this study is to develop yield models for management and to serve as a basis for future studies into the yield of crimean pine plantations in Turkey. From this regard, there is a need for a reliable system for yield prediction to provide a firm basis for management and decision making.
Data were collected from a total of 115 sample plots from 115 plantations ranging in ages from 3 to 50 years. Plantations were stratified into five years age classes and sampled with an effort to equal allocation of at least tree sample plantations to each age grouped. For each age group, effort was also made to include the full range of site conditions (from the poorest to the best). A pre-sample inspection was done to assess the conditions of each sampled plantation. Plots were thinned and located on three different sites. Data for this study were obtained from crimean pine plantations which have the same spacing (3x1.5 m). Rectangular plots area varied from 165 to 600 m2.
For each plots, all trees (alive or dead) were measured for diameter at breast height, diameter at stump level, total height and age. For each plot, slope, altitude and aspect were also measured.
Stand characteristics were computed from individual tree measurements in the plots. Volume per hectare (V), Basal Area (BA), quadratic mean diameter (![]() ), mean height weighted by basal area (
), mean height weighted by basal area (![]() ) and number of trees per hectare (N) were given in Table 1.
) and number of trees per hectare (N) were given in Table 1.
Site index: Site index based on top height/plantation age was the basis of classifying plantations into site classes. The proportional curves method described by Alder (1980) was used. A single equation was fitted to the plot level top height (the average height of the largest 100 trees per hectare)-age data, using following models:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where Hdom is the top height; A the age (years); β is a regression coefficient and k is a constant. A value for k = 1/2 was determined iteratively using non-linear regressions.
| Table 1: | Mean, SD, range of main characteristics in the study material |
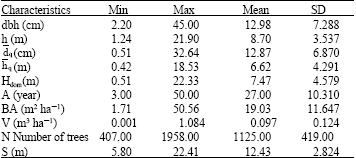 | |
SD: Standard Deviation, dbh and h is diameter at breast height and total height of individual trees in sample plots; | |
From these models, the model having the highest coefficient of determination and the lowest standard error was chosen as site index model.
Anamorphic curves were drawn from the guide curve, using the top height reached at a reference age, which has been established at 40 years for this study.
The best guide curve thus obtained was defined as the average site quality class. Then, two more site quality classes were defined, one above (best class) and one below (worst class).
Yield models: The development of these tables requires different expressions representing relationships among stand variables. The variables used in this study are: age (years), number of stems per hectare, quadratic mean dbh (cm), mean height (m), basal area (m2 ha–1), volume (m3 ha–1). In preparing these models, the methodology used in yield tables (Laurie and Ram, 1940; Maitre, 1983) was followed.
The first relationship is of Hdom = f (age), which was obtained during the development of site index curves (Hdom is top height).
In this study, a general yield equation (e.g., Schumacher type) was not used for the development of the yield models. The measures of yield (quadratic mean dbh, mean height, basal area, number of trees and volume) were prepared based on age and site index and their transformations as a predictor and possible insignificant predictors were excluded. The predicted variables in the yield models were quadratic mean diameter, mean height, number of trees, basal area and volume, which resulted in a linear relationship between the dependent and independent variables. All predictors had to be significant at the 0.05 level without any systematic errors in residuals.
The following model was hypothesized:
| (8) |
where S1 is the site index and S2 is the age.
Relationship between measures of yield obtained from sample plots and site index and age have been used to model yield, using stepwise procedure in Regression Analysis Method the significance of parameter estimates was tested by means of t = b/ASE, where b is the parameter estimate, t is the Student’ t and ASE is the asymptotic standard error. The parameters of the model for the data were determined using Stepwise Regression Analysis in SAS software (SAS Institute Inc., 1999). Only were variables which were significant (p<0.05) included in yield models. The assumption of homoscedasticity was tested using the Durbin-Whatson test.
Removed stand volume: For this aim, at each measurement time, both dead and cut trees were determined and measured diameter at the breast height and stump level and heights. Then, the volumes of these trees were calculated using double-entry volume table constructed by Gülen (1959). This volume converted to hectare is the removed stand volume. Obtained removed stand volume were related to stand age and site index.
The removed stand volume was as follows.
| (9) |
where Vremoved is removed stand volume (m3 per ha); A and S stand age and site index, respectively.
Parameters of the removed stand volume model were estimated using stepwise regression in SAS software (SAS Institute Inc., 1999).
Mean annual volume increment (MAI) was determined as the ratio of the volume yield model to age. The Current Annual Increment (CAI) model was obtained as a derivative of volume yield model with respect to age. From these, the ages of maximum MAI and CAI were determined.
Site index: The site index curves are presented in Fig. 1 and the equation was estimated as:
| (10) |
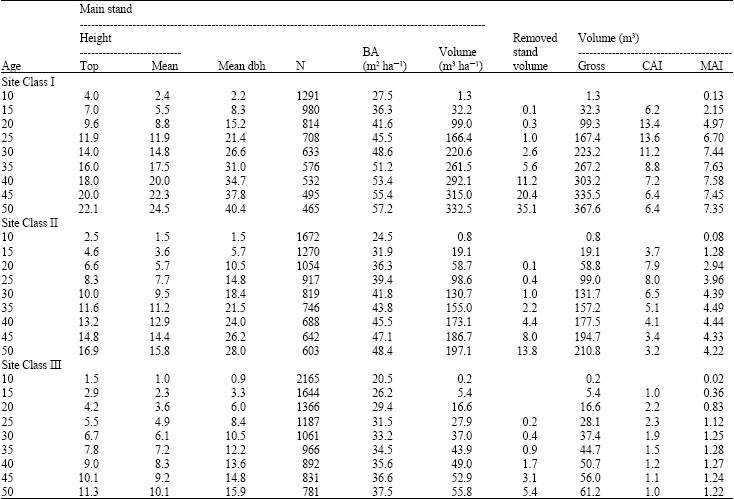
where Hdom is the top height of the plantation. Site index is top height of the plantation at the base age of 40 years. From Eq. 10, site indices of 20.5, 14.5 and 8.5 m are estimated at the base age to correspond with site classes I, II and III, respectively. In addition, by using this equation, five year intervals from age 10 to 50 and 2 m intervals from site index table was given in Table 2.
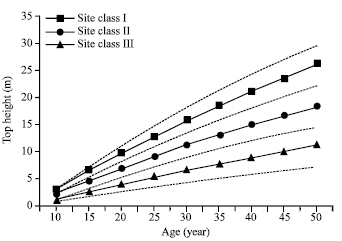 | |
| Fig. 1: | Site index curves for crimean pine plantations |
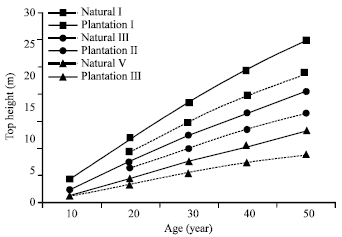 | |
| Fig. 2: | Comparison of average top heights of crimean pine plantations with figures from the natural crimean pine yield tables (Kalıpsız, 1963) for site classes I, III and V (solid lines represent curves from the study area) |
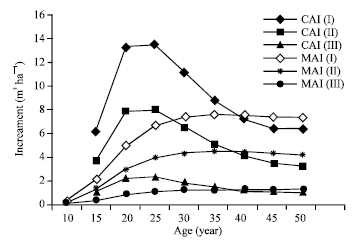 | |
| Fig. 3: | Current and mean annual increments of volume for different site index of crimean pine (MAI: Mean Annual Increment of volume; CAI: Current Annual Increment of volume) |
| Table 2: | Site index table for crimean pine plantations |
 | |
| Table 3: | Regression coefficients for each yield models for crimean pine |
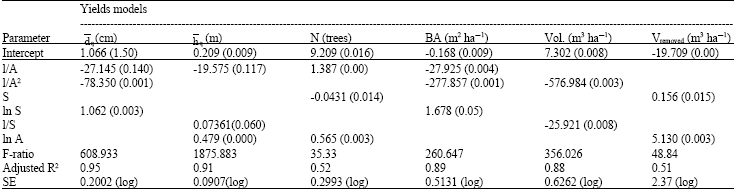 | |
| Standard errors of estimates are given in parenthesis | |
| Table 4: | Yield tables for crimean pine plantations |
 | |
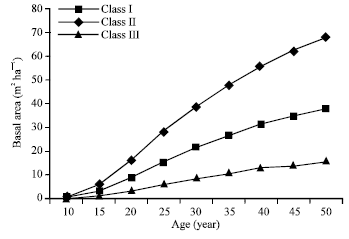 | |
| Fig. 4: | Basal area (m2 ha–1) for main stand for different site qualities |
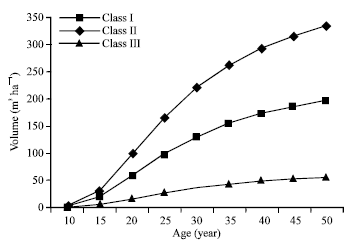 | |
| Fig. 5: | Volume (m3 ha–1) for main stand for different site qualities |
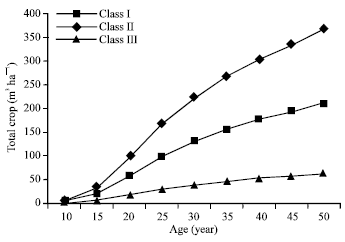 | |
| Fig. 6: | Total crop (m3 ha–1) for different site qualities |
Figure 2 is a comparison of the average top height predicted in this study with figures from the natural crimean pine yield tables for site classes I, III and V (Kalıpsız, 1963). Apparently, the curves show a similar trend.
Yield models: The regression coefficients of the yield models are given in Table 3 (Standard errors of estimates are given in parenthesis). All parameter estimates were highly significant (p<0.001) in yield models. The yield tables are presented in Table 4.
CAI and MAI are estimated to peak at ages; 21 and 35, 23 and 36 and 27 and 37, respectively for site classes I, II and III. The peak ages for the MAI may be the biologically optimum rotation ages under the current management regimes.
Figure 3 shows the evolution of mean and current annual increments of volume for different qualities of crimean pine plantations.
Volume and basal area for the main stand and total crop for different site qualities are shown in Fig. 4-6. These figures provide useful information for forest management and enable rapid and schematic comparisons to be made of the evolution of these important variables, according to site quality and stand age.
At the estimated biologically optimum rotation ages, the estimated MAI of 7.64, 4.49 and 1.28 m3 ha–1 for site classes I, II and III respectively, indicates a significant growth potential for crimean pine plantations. The estimated mean diameters and heights (Table 3) indicates that electric transmission pole size trees could be obtained from all site classes at the various biologically optimum rotations. However, with the adoption of suitable thinning schedules, it may be possible to obtain trees of even higher quality sizes at extended rotation ages, although it may not be economically, a good practice to extend rotations beyond these ages. These tables could be easily and reliably adopted as a guide for managing crimean pine and could form a useful basis for future studies.
Prominent differences observed in Fig. 2 could be attributed to methodological differences in site index curves development or differences in growth patterns. Curves in the present study were developed temporary plots, with the assumptions that, there is equal likelihood of representation of all site qualities in all age groups. Thanks to efforts were made at achieving this, it can be guaranteed for all age classes were sufficient number of plantations were found. Meanwhile, site classification based on these curves could be reliably adopted for management purposes.
The site index curves in Fig. 1 could be reliably adopted for the management of crimean pine plantations. At the reference age of 40, average site indices of 20.5, 14.5 and 8.5 m are estimated for crimean pine plantation for site classes I, II and III, respectively.
The estimated biologically optimum rotation ages for classes I, II and III are 35, 36 and 37 years, respectively. The MAI at the ages indicates a considerable growth potential for crimean pine.