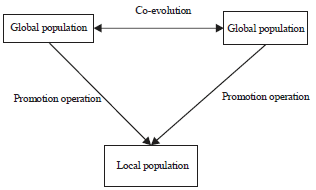
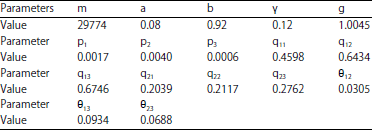
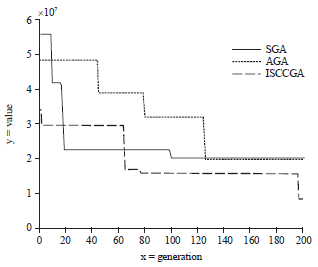
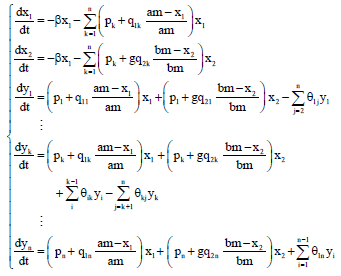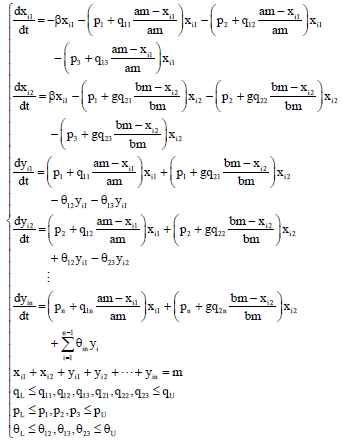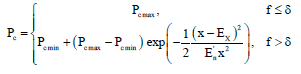Case Study
A Self-adaptive Cloud Co-evolution Genetic Algorithm for Parameter Identification of Advanced Manufacturing Mode Diffusion
School of Management Engineering, Zhengzhou University, Zhengzhou, 450001 Henan, China
Sheng Yu
School of Management Engineering, Zhengzhou University, Zhengzhou, 450001 Henan, China
Cao Haiwang
Department of Electronic and Communication Engineering, Zhengzhou Institute of Aeronautical Industry Management, 450015 Zhengzhou, China