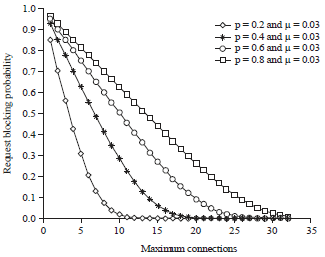
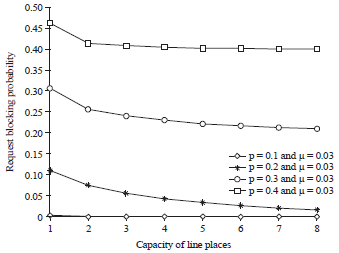
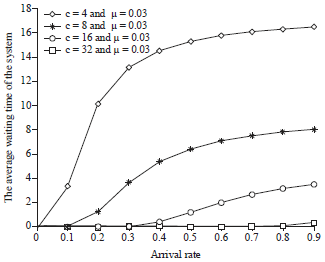
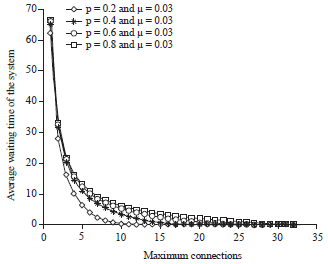
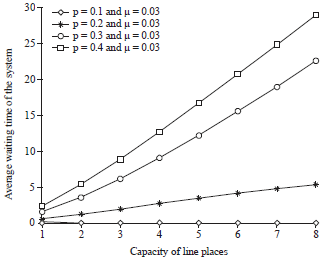
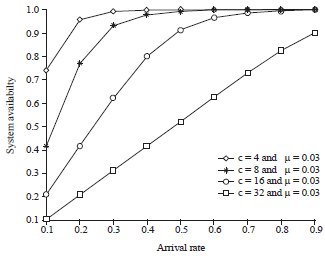
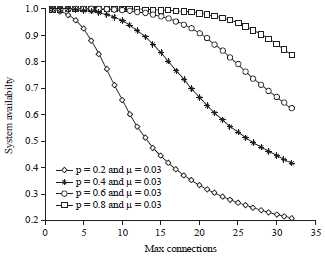
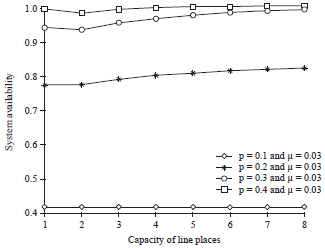
Research Article
Performance Analysis of Database Connection Pool Technology Based on Queueing Model with Mixed Waiting and Loss
School of Computer Science and Technology, Henan Polytechnic University, 454000 Jiaozuo, China
Zhanqiang Huo
School of Computer Science and Technology, Henan Polytechnic University, 454000 Jiaozuo, China